
| A. | 44 | B. | 45 | C. | 46 | D. | 無法確定 |
分析 1是第$\frac{1+1}{2}$=1個數、3是第$\frac{3+1}{2}$=2個數、5是第$\frac{5+1}{2}$=3個數…2011是第$\frac{2011+1}{2}$=1006個數.仔細觀察不難發現,這是一列相鄰奇數,從左到右分組,第一組1個,第二組2個,第三組3個…第n組n個;前一組共1個數,前二組共1+2=3個數,前三級共有1+2+3=6個數…前n項共有1+2+3+…+(n-1)個數,即前n項共有$\frac{n(n+1)}{2}$個數.令$\frac{n(n+1)}{2}$=1006,求n,應用小學知識無法解答,我們令n等于一個值時,求出前n組的個數,再看第1006個數在第幾組.
解答 解:$\frac{2011+1}{2}$=$\frac{2012}{2}$=1006
即2011是第1006個數
前n項共有$\frac{n(n+1)}{2}$個數
當n=44時,$\frac{44×(44+1)}{2}$=$\frac{44×45}{2}$=$\frac{1980}{2}$=990
當n=45時$\frac{45×(45+1)}{2}$=$\frac{45×46}{2}$=$\frac{2070}{2}$=1035
990<1006<1035
所以第1006個數在第45組.
故選:B.
點評 此題用小學知識解答比較難,關鍵是先找出這些數列的規律,確定2011是第幾個數,再根據前n項組和的公式看在第幾組.


科目:小學數學 來源: 題型:解答題
查看答案和解析>>
科目:小學數學 來源: 題型:計算題
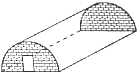 如圖,用薄膜蓋成的一個蔬菜大棚長12m,它的外形是半個圓柱,兩端是半徑為3m的半圓形磚墻,蓋這個蔬菜大棚至少需要多少平方米的薄膜?(接頭損耗忽略不計)
如圖,用薄膜蓋成的一個蔬菜大棚長12m,它的外形是半個圓柱,兩端是半徑為3m的半圓形磚墻,蓋這個蔬菜大棚至少需要多少平方米的薄膜?(接頭損耗忽略不計)查看答案和解析>>
科目:小學數學 來源: 題型:計算題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com