解答:解:根據題意可得:“好”是不為1的奇數,“好”=3,5,7,9中的一個;
一個不是1的奇數與“運”相乘所得的積的末尾還是“運”,那么,“運”只能是0或5,很明顯0不符合題意,那么,“運”=5;
假設“好”=3,3×5=15,向上一位進1;“奧”×5+1的末尾是8,也就是“奧”×5的末尾數是8-1=7,找不到一個數與5相乘的積的末尾數7,因此,“好”不是3;
假設“好”=5,與“運”=5重復,因此,“好”不是3;
假設“好”=9,9×5=45,向上一位進4;“奧”×5+4的末尾是8,也就是“奧”×5的末尾數是8-4=4,找不到一個數與5相乘的積的末尾數4,因此,“好”不是9;
由以上可以得出:“好”=7;
十位上,7×5=35,向上一位進3;“奧”×5+3的末尾是8,也就是“奧”×5的末尾數是8-3=5,那么,“奧”代表的數是奇數,并且只能是1,3或9,5與7被“運”和“好“所用;
假設“奧”=9,9×5+3=48,向上一位進4;“博”×5+4的末尾是0,也就是“博”×5的末尾是10-4=6,找不到一個數與5相乘的積的末尾數6,因此,“奧”不是9;
假設“奧”=3,3×5+3=18,向上一位進1;“博”×5+1的末尾是0,也就是“博”×5的末尾是10-1=9,找不到一個數與5相乘的積的末尾數9,因此,“奧”不是3;
由以上可以得出:“奧”=1;
1×5+3=8;“博”×5的末尾是0,“博”只能是偶數,也就是“”是0,2,4,6,8中的一個;
假設“博”=8,8×5=40,向上一位進4;“海”×5+4末尾是0,也就是“海”×5的末尾是10-4=6,找不到一個數與5相乘的積的末尾數6,因此,“海”不是8;
假設“博”=6,6×5=30,向上一位進3;“海”×5+3末尾是0,也就是“海”×5的末尾是10-3=7,找不到一個數與5相乘的積的末尾數7,因此,“海”不是6;
假設“博”=4,4×5=20,向上一位進2;“海”×5+2末尾是0,也就是“海”×5的末尾是10-2=8,找不到一個數與5相乘的積的末尾數8,因此,“海”不是4;
假設“博”=2,2×5=10,向上一位進1;“海”×5+1末尾是0,也就是“海”×5的末尾是10-1=9,找不到一個數與5相乘的積的末尾數9,因此,“海”不是2;
由以上可得:“博”=0;
0×5=0;“海”×5的末尾是0,“海”只能是0除外的偶數,也就是“”是2,4,6,8中的一個;
又因為“上”×5加上“海”×5的進位結果是12,只有2×5+2=12,也就是“海”×5進位是2,4×5=20,進位是2,所用,“海”=4,“上”=2;
由以上分析可得豎式是:
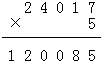
;
所以,“上海博奧好”所代表的數是:24017.

 如圖的算式中,相同的漢字代表相同的數字,不同的漢字代表不同的數字,且“好”是不為1的奇數,那么此算式成立時“上海博奧好”所代表的數是多少?
如圖的算式中,相同的漢字代表相同的數字,不同的漢字代表不同的數字,且“好”是不為1的奇數,那么此算式成立時“上海博奧好”所代表的數是多少?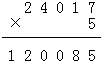 ;
;

 閱讀快車系列答案
閱讀快車系列答案 在如圖的算式中,相同的漢字代表相同的數字,不同的漢字代表0-9中不同的數字,這些漢字各代表哪些數字?
在如圖的算式中,相同的漢字代表相同的數字,不同的漢字代表0-9中不同的數字,這些漢字各代表哪些數字? ①下面兩個算式中,相同的漢字代表相同的數字,不同的漢字代表不同的數字.美×
①下面兩個算式中,相同的漢字代表相同的數字,不同的漢字代表不同的數字.美×