Question

圖中陰影部分的面積是5平方厘米，求圓環的面積

Answer 1

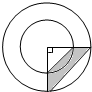
考點：圓、圓環的面積

專題：平面圖形的認識與計算

分析：由圖可以看出：大等腰直角三角形的面積-小等腰直角三角形的面積=陰影的面積=5平方厘米，因為三角形的直角邊是內外圓的半徑，所以根據三角形的面積差，可以求出環形半徑的平方差，然后根據圓環的面積=大圓的面積-小圓的面積，利用圓環的面積公式求得即可．

解答： 解：設大圓的半徑為R，小圓的半徑為r，
陰影的面積=R²÷2-r²÷2=5（平方厘米）
那么R²-r²=5×2=10（平方厘米）
圓環的面積：S_圓環=πR²-πr²
=π×（R²-r²）
=π×10
=31.4（平方厘米）；
答：圖中圓環部分的面積是31.4平方厘米．

點評：此題主要考查三角形及圓環的面積求法，利用等量代換即可．