
【題目】小麗和小明一起練習散步,路線是如圖所示的一個公共點的兩個圓形跑道.大圓的直徑為48米,小圓的直徑為30米,小麗跑小圓形跑道,小明跑大圓形跑道.某天,他們倆同時由A地出發,以相同的速度慢跑,當小麗跑圈時,兩個人相距最遠. 
【答案】4
【解析】解:30π和24π的最小倍數,即為30與24的最小公倍數再乘以π.
30=2×3×5,24=2×2×2×3;
則30與24的最小公倍數是:2×2×2×3×5=120;
120÷30=4,
120÷24=5,
即小麗在小圓上跑了4圈后,小明在大圓上跑了5個![]() 圓周長,即到了B點,此時兩個人相距最遠.
圓周長,即到了B點,此時兩個人相距最遠.
故答案為:4.
圓內的任意兩點,以直徑兩端點的距離最遠.即小麗到A點、小明到B點時,兩個人的距離最遠.小圓周長為π×30=30π,大圓周長為π×48=48π,一半為24π.問題轉化為求30π和24π的“最小公倍數”問題.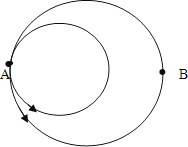


科目:小學數學 來源: 題型:
【題目】如圖,四個小三角形的頂點處有六個圓圈.如果在這些圓圈中分別填上六個質數,它們的和是20,而且每個小三角形三個頂點上的數之和相等.問這六個質數的積是多少? 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com