
 如圖,已知邊長為5的正方形ABCD和邊長為3的正方形CEFG共頂點C,正方形CEFG繞點C旋轉60°,連接BE、DG,則△BCE的面積與△CDG的面積比是________.
如圖,已知邊長為5的正方形ABCD和邊長為3的正方形CEFG共頂點C,正方形CEFG繞點C旋轉60°,連接BE、DG,則△BCE的面積與△CDG的面積比是________.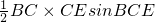 ,BC是邊長為5的正方形ABCD的邊長,所以BC=5,CE是邊長為3的正方形CEFG的邊長,所以CE=3,正方形CEFG繞點C旋轉60°,可求出∠BCE=120°,可求出△BCE的面積;同理在△CDG中根據正弦定理求出它的面積.據此可解答.
,BC是邊長為5的正方形ABCD的邊長,所以BC=5,CE是邊長為3的正方形CEFG的邊長,所以CE=3,正方形CEFG繞點C旋轉60°,可求出∠BCE=120°,可求出△BCE的面積;同理在△CDG中根據正弦定理求出它的面積.據此可解答.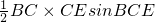 =
=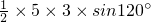 ;
;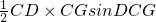 =
=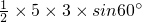 ;
;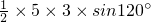 ):(
):(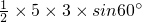 )=1:1;
)=1:1;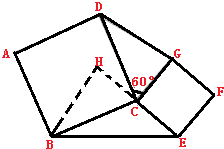
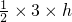 ,
,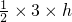 ,
,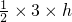 ):(
):(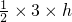 )=1:1,
)=1:1,

 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案科目:小學數學 來源: 題型:
 如圖,ABCD是邊長為5的正方形,E、F、G、H分別在邊AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE圍成的四邊形PQRS是正方形,求圖中陰影部分的面積.
如圖,ABCD是邊長為5的正方形,E、F、G、H分別在邊AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE圍成的四邊形PQRS是正方形,求圖中陰影部分的面積.查看答案和解析>>
科目:小學數學 來源: 題型:
 如圖,有一塊邊長為3米的正方形草地,在點B處用一根木樁牽住了一頭小羊.已知牽羊的繩子長2米,那么草地上不會被羊吃掉草的部分是
如圖,有一塊邊長為3米的正方形草地,在點B處用一根木樁牽住了一頭小羊.已知牽羊的繩子長2米,那么草地上不會被羊吃掉草的部分是查看答案和解析>>
科目:小學數學 來源: 題型:
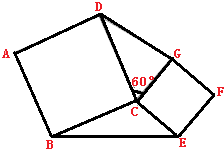 如圖,已知邊長為5的正方形ABCD和邊長為3的正方形CEFG共頂點C,正方形CEFG繞點C旋轉60°,連接BE、DG,則△BCE的面積與△CDG的面積比是
如圖,已知邊長為5的正方形ABCD和邊長為3的正方形CEFG共頂點C,正方形CEFG繞點C旋轉60°,連接BE、DG,則△BCE的面積與△CDG的面積比是查看答案和解析>>
科目:小學數學 來源: 題型:解答題
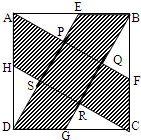 如圖,ABCD是邊長為5的正方形,E、F、G、H分別在邊AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE圍成的四邊形PQRS是正方形,求圖中陰影部分的面積.
如圖,ABCD是邊長為5的正方形,E、F、G、H分別在邊AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE圍成的四邊形PQRS是正方形,求圖中陰影部分的面積.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com