
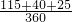 +1×6,
+1×6, +1×6,
+1×6,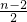 +1×2n,
+1×2n, 圓弧+半徑×2n,依此列式計算即可求解.
圓弧+半徑×2n,依此列式計算即可求解.

 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案科目:小學數學 來源: 題型:
 (2012?明光市)①請在圖1中畫出三角形ABC中AB邊上的高,并以AB邊和AC邊為平行四邊形的兩條鄰邊畫一個平行四邊形.
(2012?明光市)①請在圖1中畫出三角形ABC中AB邊上的高,并以AB邊和AC邊為平行四邊形的兩條鄰邊畫一個平行四邊形.查看答案和解析>>
科目:小學數學 來源: 題型:
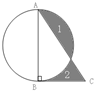 (2012?長清區模擬)在三角形abc中,∠c=90度,ab=20厘米,以ab為直徑畫圓.如果陰影(1)的面積比陰影(2)的面積大7平方厘米,求bc的長度.
(2012?長清區模擬)在三角形abc中,∠c=90度,ab=20厘米,以ab為直徑畫圓.如果陰影(1)的面積比陰影(2)的面積大7平方厘米,求bc的長度.查看答案和解析>>
科目:小學數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com