Question

8．已知正方形ABCD的面積是30平方厘米，四邊形GCEF為正方形，陰影部分的面積是15平方厘米

Answer 1

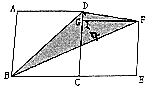
分析 如圖，分別作AD、EF的延長線相交于點H，這樣四邊形DBEH是一個梯形．陰影部分面積造型這個梯形的面積減去三角形BEF的面積，再減去三角形DHF面積．根據三角形的面積計算公式“S=$\frac{1}{2}$ah”、梯形面積計算公式“S=$\frac{1}{2}$（a+b）h”，我們再設大正方形的邊長為acm，小正方形的邊長為bcm，即可解答．

解答 解：如圖，分別作AD、EF的延長線相交于點H．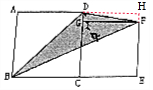

三角形BEF的面積：
$\frac{1}{2}$×（a+b）×b
三角形DHF的面積：
$\frac{1}{2}$×（a-b）×b
梯形DBEH的面積：
$\frac{1}{2}$×（b+a+b）×a
陰影部分面積：
$\frac{1}{2}$×（b+a+b）×b-$\frac{1}{2}$×（a+b）×b-$\frac{1}{2}$×（a-b）×b
=$\frac{1}{2}$×（a+2b）×a-$\frac{1}{2}$×（a+b）×b-$\frac{1}{2}$×（a-b）×b
=$\frac{1}{2}$a²
=$\frac{1}{2}$×30
=15（平方厘米）
答：陰影部分面積是15平方厘米．
故答案為：15平方厘米．

點評 此題難度較大．通過作輔助線，很容易看出陰影部分面積造型梯形面積減去兩個三角形面積，沒告訴大、小正方形的邊長，只知道大正方形的面積，設大正方形的邊長為acm，小正方形的邊長為bcm，根據三角形面積計算公式、梯形面積計算公式，用含有字母a、b的式子表示三角形、梯形的面積，通過計算最后是$\frac{1}{2}$a²，a²已知，從而求陰影部分面積．