Question

求圖中陰影部分的面積和周長．

Answer 1

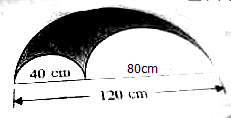
考點：組合圖形的面積

專題：平面圖形的認識與計算

分析：（1）首先求出整個大半圓的半徑是多少，進而根據圓的面積公式，求出大半圓的面積是多少；然后分別求出直徑分別是40cm和80cm的半圓的面積，最后用整個大半圓的面積減去直徑分別是40cm和80cm的圓的面積，求出陰影部分的面積是多少即可；
（2）首先根據圓的周長公式，分別求出直徑是120cm、40cm、80cm的半圓的長度，然后求和，求出陰影部分的周長是多少即可．

解答： 解：（1）3.14×（120÷2）²÷2-3.14×（40÷2）²÷2-3.14×（80÷2）²÷2
=5652-628-2512
=2512（cm²）
答：陰影部分的面積是2512cm²．

（2）3.14×120÷2+3.14×40÷2+3.14×80÷2
=188.4+62.8+125.6
=376.8（cm）
答：陰影部分的周長是376.8cm．

點評：此題主要考查了組合圖形的面積的求法，解答此題的關鍵是熟練掌握圓的周長、面積公式．