
 如右圖,跑道外圈周長400米,沿ACBA小圈跑是275米,其中A至B的直線距離是75米.甲乙兩人同時從A點出發練長跑,甲沿小圈跑,每100米用24秒,乙沿外圈跑,每100米用21秒.乙跑第________圈時第一次與甲相遇,出發后________分________秒甲、乙再次在A點相遇.
如右圖,跑道外圈周長400米,沿ACBA小圈跑是275米,其中A至B的直線距離是75米.甲乙兩人同時從A點出發練長跑,甲沿小圈跑,每100米用24秒,乙沿外圈跑,每100米用21秒.乙跑第________圈時第一次與甲相遇,出發后________分________秒甲、乙再次在A點相遇. (米/秒),乙速為100÷21=
(米/秒),乙速為100÷21=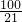 (米/秒),速度差為
(米/秒),速度差為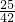 (米/秒),;
(米/秒),; =66(秒);
=66(秒);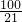 =84(秒);
=84(秒);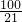 ×
×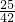 =25(米),即甲領先25÷
=25(米),即甲領先25÷ =6(秒),
=6(秒),

科目:小學數學 來源: 題型:
 如右圖,跑道外圈周長400米,沿ACBA小圈跑是275米,其中A至B的直線距離是75米.甲乙兩人同時從A點出發練長跑,甲沿小圈跑,每100米用24秒,乙沿外圈跑,每100米用21秒.乙跑第
如右圖,跑道外圈周長400米,沿ACBA小圈跑是275米,其中A至B的直線距離是75米.甲乙兩人同時從A點出發練長跑,甲沿小圈跑,每100米用24秒,乙沿外圈跑,每100米用21秒.乙跑第查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com