Question

如圖，DC=1.5AB，梯形面積為50m²．求陰影部分的面積．

Answer 1

考點：三角形面積與底的正比關系

專題：平面圖形的認識與計算

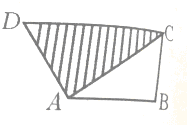
分析：由圖知，三角形ACD與三角形ABC的高相等，都等于梯形的高，又知DC=1.5AB，根據高相等的三角形面積的比等于底邊的比，得出三角形ACD與三角形ABC面積的比是1.5：1=3：2，由此把三角形ACD的面積看作3份，三角形ABC的面積就是2份，梯形的面積就是3+2=5份，則陰影部分的面積就占梯形面積的

3

5

，已知梯形面積為50m²，用乘法即可求得陰影部分的面積．

解答： 解：DC=1.5AB，則DC：AB=1.5：1=3：2，
即三角形ACD與三角形ABC面積的比是3：2，
則陰影部分的面積：50×

3

3+2

=30（m²），
答：陰影部分的面積是30m²．

點評：此題考查了高相等的三角形面積的比等于底邊的比的運用．