分析:觀察前四幅圖可得,第一幅圖是1個點;第二幅圖1+4個點,可以寫作1+1×4;第三幅1+8個點,可以寫作1+2×4;第四幅圖1+12個點,可以寫作1+3×4;由此可得第n幅圖,有1+(n-1)×4個點,由此即可解決問題.
解答:解:根據題干觀察,可以看出這組圖形的排列規律是:第n個圖形的點數為:1+(n-1)×4個點;
當n=5時,1+(5-1)×4=1+16;
所以可以接著畫出圖形為:
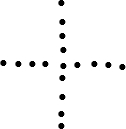
故答案為:16.
點評:此題關鍵是根據已知的圖形得出每一幅圖形的點數的排列以及個數的特點,得出一般的規律即可解決此類問題.




