【題目】如圖，正方形ABCD的邊長為4厘米，AE=2BE，求三角形CDF的面積．
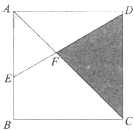
【答案】4.8平方厘米
【解析】
試題分析：由題意可知：三角形AEF與三角形ADF等高不等底，則它們的面積比就等于底的比，因為AE=2BE，AB=AD，所以AE：AB=AE：AD=AE：（AE+BE）=2：3，則三角形AEF和三角形ADF面積比=EF：DF=AE：AD=2：3，進而可以求出三角形ADF的面積：三角形AED的面積=3：5，所以三角形ADF的面積等于三角形AED的面積的
，然后用三角形ACD的面積減去三角形ADF的面積就是三角形CDF的面積．
解：由題意可知AE=2BE，AB=AD，
則AE：AB=AE：AD=AE：（AE+BE）=2：3，
所以三角形AEF和三角形ADF面積比=EF：DF=AE：AD=2：3；
三角形ADF的面積：三角形AED的面積=3：（2+3）=3：5；
三角形AED的面積為4×
×4÷2=
（平方厘米）
所以三角形ADF的面積為×=
（平方厘米）
三角形CDF的面積為4×4÷2
=8=4.8（平方厘米）；
答：三角形CDF的面積是4.8平方厘米
小學數學口算題卡脫口而出系列答案
優秀生應用題卡口算天天練系列答案
浙江之星課時優化作業系列答案科目：小學數學 來源： 題型：
【題目】根據統計表完成下面各題。
種類 | 客車 | 貨車 | 面包車 | 小轎車 |
輛數（輛） | 20 | 15 | 35 | 40 |
（1）小轎車比客車多多少輛？
（2）什么車最少，什么車最多？
（3）貨車和面包車相差多少輛？
（4）客車和貨車的總輛數和什么車同樣多？
（5）這四種車一共有多少輛？
查看答案和解析>>
科目：小學數學 來源： 題型：
【題目】四個正整數a、b、c、d都小于1000，并且組成一個四數組（a、b、c、d），如果a+4、b﹣4、c×4、d÷4也是正整數，而且都相等，那么這樣的不同四數組共有 個．
查看答案和解析>>
科目：小學數學 來源： 題型：
【題目】在橫線里填上“＞”、“＜”或“=”．
3.78÷0.99 3.78
2.6×1.01 2.6
7.2×1.3 7.2÷1.3
9.7÷1.2 9.7﹣1.2．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
