
分析 把一年12個月看作12個抽屜,把54人看作54個元素,那么每個抽屜需要放54÷12=4(個)元素,還剩余6個,余下的6人無論怎么放,總有一個抽屜至少放5個元素,因此至少有5名同學同一個月出生,據此解答.
解答 解:建立抽屜,把這12個月看做是12個抽屜,
54÷12=4(人)…6(人)
4+1=5(人)
所以至少有5人在同一個月出生.
原題說法正確.
故答案為:√.
點評 本題考查了抽屜原理:把m個元素任意放入n(n≤m)個集合,則一定有一個集合至少要有k個元素.其中 k=m÷n(當n能整除m時)或k=m÷n+1 (當n不能整除m時).


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:小學數學 來源: 題型:解答題
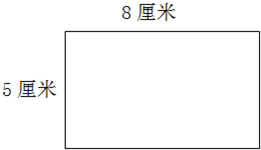 如圖,從一個長方形上剪下一個最大的正方形,
如圖,從一個長方形上剪下一個最大的正方形,查看答案和解析>>
科目:小學數學 來源: 題型:計算題
| 直接寫出得數: 0.1×12= | 2.5-1.7= | $\frac{3}{5}$÷3= | 3.25×4= |
| 0.5×(2.6-2.4)= | 2.2+3.57= | 0.9×99+0.9= |
查看答案和解析>>
科目:小學數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com