
 如圖,c=6,三個同心圓的半徑依次為
如圖,c=6,三個同心圓的半徑依次為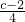 ,
, ,和
,和 ,圖中陰影部分的面積與最大圓面積的比是________.
,圖中陰影部分的面積與最大圓面積的比是________.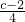 =1,
=1, =2,
=2, =3,結合圖形發現:陰影部分可以分為三部分進行計算,一是半徑為1的最小圓內圓心角為90°的扇形面積;二是內圓半徑為1,外圓半徑為2,圓心角為20°的圓環的面積,三是內圓半徑為2,外圓半徑為3,圓心角為60°的圓環的面積,由此利用扇形和圓環的面積公式即可求出陰影部分的面積,再利用圓的面積公式求出最大圓的面積即可求出它們的面積之比.
=3,結合圖形發現:陰影部分可以分為三部分進行計算,一是半徑為1的最小圓內圓心角為90°的扇形面積;二是內圓半徑為1,外圓半徑為2,圓心角為20°的圓環的面積,三是內圓半徑為2,外圓半徑為3,圓心角為60°的圓環的面積,由此利用扇形和圓環的面積公式即可求出陰影部分的面積,再利用圓的面積公式求出最大圓的面積即可求出它們的面積之比.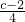 =1,
=1, =2,和
=2,和 =3,
=3, π×12+
π×12+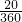 π(22-12)+
π(22-12)+ π(32-22),
π(32-22), π+
π+ π×(4-1)+
π×(4-1)+ π×(9-4),
π×(9-4), π+
π+ π+
π+ π,
π, π;
π; π:9π=5:36,
π:9π=5:36,

科目:小學數學 來源: 題型:
 如圖,有三個同心圓,它們的直徑分別為2,6,10,用線段分割成9塊,如果每塊字母代表這一塊的面積并且相同的字母代表相同的面積,那么(2A+B):C=
如圖,有三個同心圓,它們的直徑分別為2,6,10,用線段分割成9塊,如果每塊字母代表這一塊的面積并且相同的字母代表相同的面積,那么(2A+B):C=查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com