Question

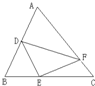
在如圖△ABC中，AD=AB，BE=BC，CF=AC．如果△DEF的面積是1，那么△ABC的面積是

1. A.
   
2. B.
   3
3. C.
   
4. D.
   4

Answer 1

B
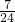
分析：如圖，連接AE，CD，因為AD=AB，可得：三角形BDE=三角形ABE，又因為BE=BC，可得三角形ABE=×三角形ABC，據此可得：三角形BDE=××三角形ABC=×三角形ABC；
同理，推出三角形ADF=×三角形ABC；三角形BFC=×三角形ABC，所以可得出三角形DEF=（1---）×三角形ABC=×三角形ABC，據此即可求出三角形ABC的面積．

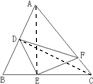
解答：連接AE，CD，因為AD=AB，可得：三角形BDE=三角形ABE，
又因為BE=BC，可得三角形ABE=×三角形ABC，
所以三角形BDE=××三角形ABC=×三角形ABC；
同理，推出三角形ADF=×三角形ABC；
三角形BFC=×三角形ABC，
所以三角形DEF=（1---）×三角形ABC=×三角形ABC，
又因為三角形DEF=1，
所以三角形ABC的面積是：3×1=3，
故選：B．
點評：此題主要考查高一定時，三角形的面積與底成正比例的性質的靈活應用．