Question

【題目】操作與計算．

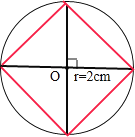
（1）在右面的空白處畫一個周長為12.56厘米的圓，并在圓內畫兩條相互垂直的直徑，然后依次連接這兩條直徑的四個端點，得到一個正方形，這個正方形的面積是　 　平方厘米．

（2）畫出如圖的對稱軸．（有幾條畫幾條）

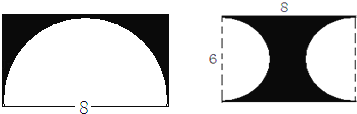
（3）求各圖陰影部分的面積．（單位：dm）

Answer 1

【答案】如圖，正方形的面積是8平方厘米．陰影部分的面積分別為6.88平方厘米和19.74平方厘米

【解析】

試題分析：（1）先根據圓的周長求出圓的半徑，由半徑畫出我們所需的圓，然后畫兩條相互垂直的直徑，最后依次連接這兩條直徑的四個端點，得到一個正方形，再根據圓的內接四邊形和小三角形的關系求出正方形的面積來．

（2）依據軸對稱圖形的意義，即在平面內，如果一個圖形沿一條直線對折，對折后的兩部分都能完全重合，這樣的圖形叫做軸對稱圖形，這條直線就是其對稱軸，據此即可進行解答．

（3）左邊圖形中陰影部分的面積=長方形的面積﹣半圓的面積，又因長方形的長等于半圓的直徑，寬等于半圓的半徑；右邊圖形中陰影部分的面積=長方形的面積﹣圓的面積，圓的直徑等于長方形的寬，于是利用長方形和圓的面積公式即可求解．

解：（1）由題意知，周長為12.56厘米的圓的半徑為：

12.56÷π÷2，

=12.56÷3.14÷2，

=2（厘米）；

半徑為2厘米的圓如下圖所示：

正方形的面積為：4×（2×2÷2）=8（平方厘米）；

答：這個正方形的面積是8平方厘米．

（2）據分析畫圖形的對稱軸如下所示：

（3）左邊圖形中陰影部分的面積為：

8×（8÷2）﹣3.14×（8÷2）2÷2，

=32﹣3.14×16÷2，

=32﹣25.12，

=6.88（平方厘米）；

右邊圖形中陰影部分的面積是：

8×6﹣3.14×（6÷2）2，

=48﹣3.14×9，

=48﹣28.26，

=19.74（平方厘米）；

答：陰影部分的面積分別為6.88平方厘米和19.74平方厘米．

故答案為：8．