
抽象函數的性質所對應的一些具體特殊函數模型:
①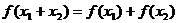
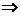 正比例函數
正比例函數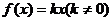
②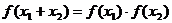 ;
;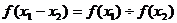
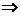 指數函數
指數函數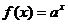 ;
;
③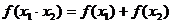 ;
;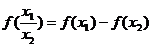
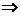 對數函數
對數函數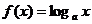 ;
;
課本題
1.設集合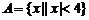 ,
,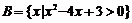 ,則集合{
,則集合{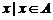 且
且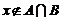 }=[1,3]。
}=[1,3]。
定義域:{x|x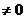 };值域:
};值域: ; 奇偶性:奇函數;
; 奇偶性:奇函數;
單調性: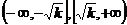 是增函數;
是增函數;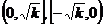 是減函數。
是減函數。
(1)一元一次函數: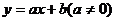 ,當
,當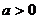 時,是增函數;當
時,是增函數;當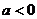 時,是減函數;
時,是減函數;
(2)一元二次函數:
一般式: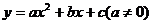 ;對稱軸方程是x=-
;對稱軸方程是x=-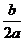 ;頂點為(-
;頂點為(-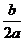 ,
,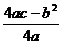 );
);
兩點式: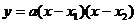 ;對稱軸方程是x=
;對稱軸方程是x=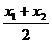 與
與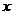 軸交點(x
軸交點(x ,0)(x
,0)(x ,0);
,0);
頂點式: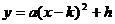 ;對稱軸方程是x=k;頂點為(k,h);
;對稱軸方程是x=k;頂點為(k,h);
①一元二次函數的單調性:
當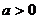 時:(-
時:(-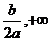 )為增函數;(-
)為增函數;(-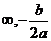 )為減函數;
)為減函數;
當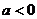 時:(-
時:(-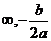 )為增函數;(-
)為增函數;(-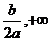 )為減函數;
)為減函數;
②二次函數求最值問題:首先要采用配方法,化為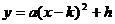 的形式,
的形式,
有三個類型題型:(1)頂點固定,區間也固定。如: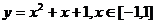
(2)頂點含參數(即頂點變動),區間固定,這時要討論頂點橫坐標何時在區間之內,何時在區間之外。(3)頂點固定,區間變動,這時要討論區間中的參數.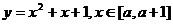 ③二次方程實數根的分布問題: 設實系數一元二次方程
③二次方程實數根的分布問題: 設實系數一元二次方程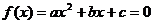 的兩根為
的兩根為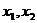
(3)反比例函數:
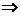
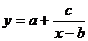
(4)指數函數: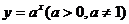
指數運算法則: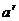 ·
·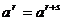 ;
; 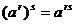 ;
; 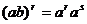 。
。
指數函數:y=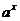 (a>o,a≠1),圖象恒過點(0,1),單調性與a的值有關,在解題中,往往要對a分a>1和0<a<1兩種情況進行討論,要能夠畫出函數圖象的簡圖。
(a>o,a≠1),圖象恒過點(0,1),單調性與a的值有關,在解題中,往往要對a分a>1和0<a<1兩種情況進行討論,要能夠畫出函數圖象的簡圖。
(5)對數函數: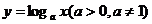
對數運算法則: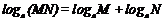 ;
;
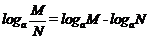 ;
; 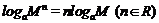
對數函數:y=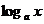 (a>o,a≠1) 圖象恒過點(1,0),單調性與a的值有關,在解題中,往往要對a分a>1和0<a<1兩種情況進行討論,要能夠畫出函數圖象的簡圖。
(a>o,a≠1) 圖象恒過點(1,0),單調性與a的值有關,在解題中,往往要對a分a>1和0<a<1兩種情況進行討論,要能夠畫出函數圖象的簡圖。
注意:
(1)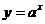 與
與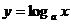 的圖象關系是關于y=x對稱;
的圖象關系是關于y=x對稱;
(2)比較兩個指數或對數的大小的基本方法是構造相應的指數或對數函數,若底數不相同時轉化為同底數的指數或對數,還要注意與1比較或與0比較。
(3)已知函數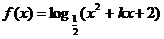 的定義域為
的定義域為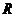 ,求
,求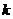 的取值范圍。(-2
的取值范圍。(-2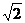 ,2
,2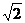 )
)
已知函數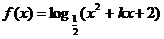 的值域為
的值域為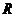 ,求
,求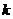 的取值范圍。
的取值范圍。
常見圖像變化規律:(注意平移變化能夠用向量的語言解釋,和按向量平移聯系起來思考)
平移變換 y=f(x)→y=f(x+a),y=f(x)+b
注意:(ⅰ)有系數,要先提取系數。如:把函數y=f(2x)經過左移2個單位平移得到函數y=f(2x+4)的圖象。
(ⅱ)會結合向量的平移,理解按照向量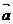 (m,n)平移的意義。
(m,n)平移的意義。
對稱變換 y=f(x)→y=f(-x),關于y軸對稱
y=f(x)→y=-f(x) ,關于x軸對稱
y=f(x)→y=f|x|,把x軸上方的圖象保留,x軸下方的圖象關于x軸對稱
y=f(x)→y=|f(x)|把y軸右邊的圖象保留,然后將y軸右邊部分關于y軸對稱。
(注意:它是一個偶函數)
伸縮變換:y=f(x)→y=f(ωx),
y=f(x)→y=Af(ωx+φ)具體參照三角函數的圖象變換。
一個重要結論:若f(a-x)=f(a+x),則函數y=f(x)的圖像關于直線x=a對稱;
函數的單調性、奇偶性、周期性
單調性:定義:注意定義是相對與某個具體的區間而言。
判定方法有:定義法(作差比較和作商比較)
導數法(適用于多項式函數)
復合函數法和圖像法。
應用:比較大小,證明不等式,解不等式。
奇偶性:定義:注意區間是否關于原點對稱,比較f(x) 與f(-x)的關系。f(x) -f(-x)=0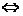 f(x) =f(-x)
f(x) =f(-x) 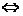 f(x)為偶函數;
f(x)為偶函數;
f(x)+f(-x)=0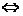 f(x) =-f(-x)
f(x) =-f(-x) 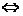 f(x)為奇函數。
f(x)為奇函數。
判別方法:定義法, 圖像法 ,復合函數法
應用:把函數值進行轉化求解。
周期性:定義:若函數f(x)對定義域內的任意x滿足:f(x+T)=f(x),則T為函數f(x)的周期。
其他:若函數f(x)對定義域內的任意x滿足:f(x+a)=f(x-a),則2a為函數f(x)的周期.
應用:求函數值和某個區間上的函數解析式。
相同函數的判斷方法:①定義域相同;②對應法則一樣 (兩點必須同時具備)
(1)函數解析式的求法:
①定義法(拼湊):②換元法:③待定系數法:④賦值法:
(2)函數定義域的求法:
①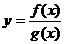 ,則g(x)
,則g(x)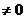 ; ②
; ②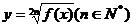 則f(x)
則f(x)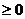 ;
;
③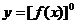 ,則f(x)
,則f(x)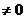 ; ④如:
; ④如: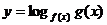 ,則
,則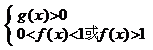 ;
;
⑤含參問題的定義域要分類討論;
⑥對于實際問題,在求出函數解析式后;必須求出其定義域,此時的定義域要根據實際意義來確定。如:已知扇形的周長為20,半徑為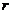 ,扇形面積為
,扇形面積為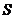 ,則
,則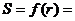 -r
-r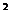 +10r;定義域為(0,10)。
+10r;定義域為(0,10)。
(3)函數值域的求法:
①配方法:轉化為二次函數,利用二次函數的特征來求值;常轉化為型如: 的形式;
的形式;
②逆求法(反求法):通過反解,用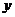 來表示
來表示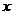 ,再由
,再由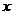 的取值范圍,通過解不等式,得出
的取值范圍,通過解不等式,得出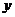 的取值范圍;常用來解,型如:
的取值范圍;常用來解,型如: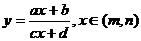 ;
;
④換元法:通過變量代換轉化為能求值域的函數,化歸思想;
⑤三角有界法:轉化為只含正弦、余弦的函數,運用三角函數有界性來求值域;
⑥基本不等式法:轉化成型如: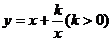 ,利用平均值不等式公式來求值域;
,利用平均值不等式公式來求值域;
⑦單調性法:函數為單調函數,可根據函數的單調性求值域。
⑧數形結合:根據函數的幾何圖形,利用數型結合的方法來求值域。
求下列函數的值域:①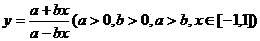 (2種方法);
(2種方法);
②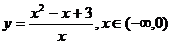 (2種方法);③
(2種方法);③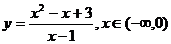 (2種方法);
(2種方法);
(1)映射的概念: (2)一一映射:(3)函數的概念:
如:若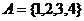 ,
,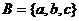 ;問:
;問: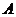 到
到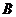 的映射有3
的映射有3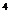 個,
個,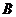 到
到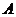 的映射有4
的映射有4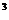 個;
個;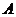 到
到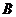 的函數有81個,若
的函數有81個,若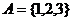 ,則
,則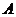 到
到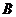 的一一映射有6個。
的一一映射有6個。
函數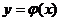 的圖象與直線
的圖象與直線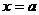 交點的個數為 0 或1個。
交點的個數為 0 或1個。
24.已知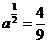 (a>0) ,則
(a>0) ,則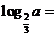 .
.
25已知函數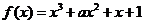 ,
,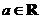 .
.
(Ⅰ)討論函數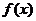 的單調區間;
的單調區間;
(Ⅱ)設函數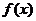 在區間
在區間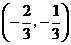 內是減函數,求
內是減函數,求 的取值范圍.
的取值范圍.
23.已知函數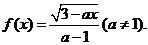
(1)若a>0,則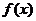 的定義域是
;
的定義域是
;
(2) 若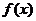 在區間
在區間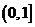 上是減函數,則實數a的取值范圍是
.
上是減函數,則實數a的取值范圍是
.
22. 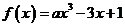 對于
對于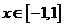 總有
總有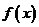 ≥0 成立,則
≥0 成立,則 = .
= .
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com