題目列表(包括答案和解析)
函數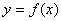
是定義在R上的奇函數，當
，
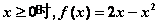（Ⅰ）求x<0時，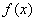
的解析式；
（Ⅱ）問是否存在這樣的正數a，b，當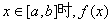
的值域為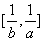
？若存在，求出所有的a，b的值；若不存在說明理由.
本小題滿分14分）
三次函數
的圖象如圖所示，直線BD∥AC，且直線BD與函數圖象切于點B，交于點D，直線AC與函數圖象切于點C，交于點A．
（1）若函數f(x)為奇函數且過點（1，-3），當x<0時求
的最大值 ；
（2）若函數在x=1處取得極值-2，試用c表示a和b，并求
的單調遞減區間；
（3）設點A、B、C、D的橫坐標分別為
，
，
，
求證
；
（本小題滿分12分）
設有兩個命題p：關于x的不等式
（a
> 0，且a ≠ 1）的解集是{ x | x < 0 }；
q：函數
的定義域為R．如果
為真命題，
為假命題，
求實數a的取值范圍．
f(x)是定義在R上的函數，對x，y∈R都有f(x＋y)＝f(x)＋f(y)，且當x>0時，f(x)<0，f(－1)＝2.
(1)求證：f(x)為奇函數；
(2)求證：f(x)是R上的減函數；
(3)求f(x)在[－2,4]上的最值．
小波以游戲方式決定是去打球、唱歌還是去下棋.游戲規則為:以O為起點,再從A1,A2,A3,A4,A5,A6(如圖)這6個點中任取兩點分別為終點得到兩個向量,記這兩個向量的數量積為X,若X>0就去打球,若X=0就去唱歌,若X<0就去下棋.
(1)寫出數量積X的所有可能取值;
(2)分別求小波去下棋的概率和不去唱歌的概率.
一、選擇題
|
的交點個數. 
可得答案C. 
代入檢驗即可. 
，不合題意，A的函數在區間
上為增函數，不合題意
可得答案B、C不正確
，故選A. 
，故選A. 
滿足
，故a的取值范圍是
，故選D. 
解析：∵
，當且僅當
時取等號. 
，
軸交于兩點等價于
，
故命題Q為真時，
端點取了開區間，扣2分）
，得M（20，24） 
解得：
∴C=60° 
=25－3ab
①
…………3分
，
上單調遞增，x<6，
，函數在（3，6）上單調遞減
取得最小值即SAMPN取得最小值24（平方米）
時等號成立. 
為偶函數， ∴
圖像與x軸恰有兩個不同的交點
為單調增函數，故
不可能有兩實根
遞減，
處取到極大值
軸有兩個交點當且僅當
，故實數a的取值范圍（0，
）
與直線
交點的個數. 
時，
遞增與直線y=ax下降或是x國，
