
題目列表(包括答案和解析)
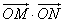 =0,其中點(diǎn)O為坐標(biāo)原點(diǎn).
=0,其中點(diǎn)O為坐標(biāo)原點(diǎn).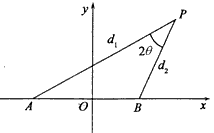
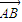 =
=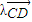 (實(shí)數(shù)λ≠0),證明:
(實(shí)數(shù)λ≠0),證明: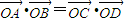 (O是坐標(biāo)原點(diǎn));
(O是坐標(biāo)原點(diǎn));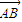 =
=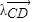 (實(shí)數(shù)λ≠0),證明:
(實(shí)數(shù)λ≠0),證明: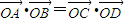 (O是坐標(biāo)原點(diǎn));
(O是坐標(biāo)原點(diǎn));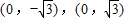 的距離之和為4,設(shè)點(diǎn)P的軌跡為C,直線y=kx+1與C交于A,B兩點(diǎn).
的距離之和為4,設(shè)點(diǎn)P的軌跡為C,直線y=kx+1與C交于A,B兩點(diǎn).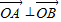 ,求k的值;
,求k的值;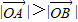 .
.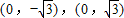 的距離之和為4,設(shè)點(diǎn)P的軌跡為C,直線y=kx+1與C交于A,B兩點(diǎn).
的距離之和為4,設(shè)點(diǎn)P的軌跡為C,直線y=kx+1與C交于A,B兩點(diǎn).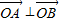 ,求k的值;
,求k的值; .
.一、選擇題
1.C 2.B 3.B 4.D 5.B 6.C
7.D 8.C 9.C 10.C
二、填空題
11.學(xué)第二次模擬考試.files/image213.gif) 12.
12.學(xué)第二次模擬考試.files/image215.gif) 13.
13.學(xué)第二次模擬考試.files/image217.gif) 14.2 15.30°
14.2 15.30°
三、解答題
16.解:(Ⅰ)由學(xué)第二次模擬考試.files/image157.gif) ,根據(jù)正弦定理得
,根據(jù)正弦定理得學(xué)第二次模擬考試.files/image220.gif) ,所以
,所以學(xué)第二次模擬考試.files/image222.gif) ,
,
由學(xué)第二次模擬考試.files/image224.gif) 為銳角三角形得
為銳角三角形得學(xué)第二次模擬考試.files/image226.gif) .………………………………………………7分
.………………………………………………7分
(Ⅱ)根據(jù)余弦定理,得學(xué)第二次模擬考試.files/image228.gif)
學(xué)第二次模擬考試.files/image230.gif)
學(xué)第二次模擬考試.files/image232.gif) .
.
所以,學(xué)第二次模擬考試.files/image234.gif) .………………………………………………14分
.………………………………………………14分
17.解:(Ⅰ)記學(xué)第二次模擬考試.files/image141.gif) 表示事件:“
表示事件:“學(xué)第二次模擬考試.files/image213.gif) 位顧客中至少
位顧客中至少學(xué)第二次模擬考試.files/image238.gif) 位采用一次性付款”,則
位采用一次性付款”,則學(xué)第二次模擬考試.files/image240.gif) 表示事件:“
表示事件:“學(xué)第二次模擬考試.files/image213.gif) 位顧客中無人采用一次性付款”.
位顧客中無人采用一次性付款”.
學(xué)第二次模擬考試.files/image243.gif) ,
,
學(xué)第二次模擬考試.files/image245.gif) .………………………………………………7分
.………………………………………………7分
(Ⅱ)記學(xué)第二次模擬考試.files/image247.gif) 表示事件:“
表示事件:“學(xué)第二次模擬考試.files/image213.gif) 位顧客每人購買
位顧客每人購買學(xué)第二次模擬考試.files/image238.gif) 件該商品,商場獲得利潤不超過
件該商品,商場獲得利潤不超過學(xué)第二次模擬考試.files/image251.gif) 元”.
元”.
學(xué)第二次模擬考試.files/image253.gif) 表示事件:“購買該商品的
表示事件:“購買該商品的學(xué)第二次模擬考試.files/image213.gif) 位顧客中無人采用分期付款”.
位顧客中無人采用分期付款”.
學(xué)第二次模擬考試.files/image256.gif) 表示事件:“購買該商品的
表示事件:“購買該商品的學(xué)第二次模擬考試.files/image213.gif) 位顧客中恰有
位顧客中恰有學(xué)第二次模擬考試.files/image238.gif) 位采用分期付款”.
位采用分期付款”.
則學(xué)第二次模擬考試.files/image260.gif) .
.
學(xué)第二次模擬考試.files/image262.gif) ,
,學(xué)第二次模擬考試.files/image264.gif) .
.
學(xué)第二次模擬考試.files/image266.gif)
學(xué)第二次模擬考試.files/image268.gif)
學(xué)第二次模擬考試.files/image270.gif)
學(xué)第二次模擬考試.files/image272.gif) .……………………………………14分
.……………………………………14分
18.解法一:(1)作學(xué)第二次模擬考試.files/image274.gif) ,垂足為
,垂足為學(xué)第二次模擬考試.files/image131.gif) ,連結(jié)
,連結(jié)學(xué)第二次模擬考試.files/image277.gif) ,由側(cè)面
,由側(cè)面學(xué)第二次模擬考試.files/image279.gif) 底面
底面學(xué)第二次模擬考試.files/image281.gif) ,得
,得學(xué)第二次模擬考試.files/image283.gif) 底面
底面學(xué)第二次模擬考試.files/image281.gif) .
.
學(xué)第二次模擬考試.files/image286.gif) 因?yàn)?sub>
因?yàn)?sub>學(xué)第二次模擬考試.files/image288.gif) ,所以
,所以學(xué)第二次模擬考試.files/image290.gif) ,又
,又學(xué)第二次模擬考試.files/image292.gif) ,故
,故學(xué)第二次模擬考試.files/image294.gif) 為等腰直角三角形,
為等腰直角三角形,學(xué)第二次模擬考試.files/image296.gif) ,
,
由三垂線定理,得學(xué)第二次模擬考試.files/image298.gif) .………………………7分
.………………………7分
(Ⅱ)由(Ⅰ)知學(xué)第二次模擬考試.files/image298.gif) ,
,
依題設(shè)學(xué)第二次模擬考試.files/image301.gif) ,
,
故學(xué)第二次模擬考試.files/image303.gif) ,由
,由學(xué)第二次模擬考試.files/image305.gif) ,
,學(xué)第二次模擬考試.files/image307.gif) ,
,學(xué)第二次模擬考試.files/image309.gif) .
.
又學(xué)第二次模擬考試.files/image311.gif) ,作
,作學(xué)第二次模擬考試.files/image313.gif) ,垂足為
,垂足為學(xué)第二次模擬考試.files/image315.gif) ,
,
則學(xué)第二次模擬考試.files/image317.gif) 平面
平面學(xué)第二次模擬考試.files/image319.gif) ,連結(jié)
,連結(jié)學(xué)第二次模擬考試.files/image321.gif) .
.學(xué)第二次模擬考試.files/image323.gif) 為直線
為直線學(xué)第二次模擬考試.files/image325.gif) 與平面
與平面學(xué)第二次模擬考試.files/image319.gif) 所成的角.
所成的角.
學(xué)第二次模擬考試.files/image328.gif)
所以,直線學(xué)第二次模擬考試.files/image325.gif) 與平面
與平面學(xué)第二次模擬考試.files/image319.gif) 所成角的正弦值為
所成角的正弦值為學(xué)第二次模擬考試.files/image332.gif) .………………………………………………14分
.………………………………………………14分
解法二:(Ⅰ)作學(xué)第二次模擬考試.files/image274.gif) ,垂足為
,垂足為學(xué)第二次模擬考試.files/image131.gif) ,連結(jié)
,連結(jié)學(xué)第二次模擬考試.files/image277.gif) ,由側(cè)面
,由側(cè)面學(xué)第二次模擬考試.files/image279.gif) 底面
底面學(xué)第二次模擬考試.files/image281.gif) ,得
,得學(xué)第二次模擬考試.files/image283.gif) 平面
平面學(xué)第二次模擬考試.files/image281.gif) .
.
因?yàn)?sub>學(xué)第二次模擬考試.files/image288.gif) ,所以
,所以學(xué)第二次模擬考試.files/image290.gif) .
.
學(xué)第二次模擬考試.files/image345.gif) 又
又學(xué)第二次模擬考試.files/image292.gif) ,
,學(xué)第二次模擬考試.files/image294.gif) 為等腰直角三角形,
為等腰直角三角形,學(xué)第二次模擬考試.files/image349.gif) .
.
如圖,以學(xué)第二次模擬考試.files/image131.gif) 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),學(xué)第二次模擬考試.files/image352.gif) 為
為學(xué)第二次模擬考試.files/image032.gif) 軸正向,建立直角坐標(biāo)系
軸正向,建立直角坐標(biāo)系學(xué)第二次模擬考試.files/image355.gif) ,
,
因?yàn)?sub>學(xué)第二次模擬考試.files/image357.gif) ,
,學(xué)第二次模擬考試.files/image359.gif) ,
,
又學(xué)第二次模擬考試.files/image172.gif) ,所以
,所以學(xué)第二次模擬考試.files/image362.gif) ,
,
學(xué)第二次模擬考試.files/image364.gif) ,
,學(xué)第二次模擬考試.files/image366.gif) .
.
學(xué)第二次模擬考試.files/image368.gif) ,
,學(xué)第二次模擬考試.files/image370.gif) ,
,學(xué)第二次模擬考試.files/image372.gif) ,
,學(xué)第二次模擬考試.files/image374.gif) ,所以
,所以學(xué)第二次模擬考試.files/image298.gif) .…………………7分
.…………………7分
(Ⅱ)學(xué)第二次模擬考試.files/image377.gif) ,
,學(xué)第二次模擬考試.files/image379.gif) .
.
學(xué)第二次模擬考試.files/image381.gif) 與
與學(xué)第二次模擬考試.files/image383.gif) 的夾角記為
的夾角記為學(xué)第二次模擬考試.files/image385.gif) ,
,學(xué)第二次模擬考試.files/image325.gif) 與平面
與平面學(xué)第二次模擬考試.files/image388.gif) 所成的角記為
所成的角記為學(xué)第二次模擬考試.files/image078.gif) ,因?yàn)?sub>
,因?yàn)?sub>學(xué)第二次模擬考試.files/image381.gif) 為平面
為平面學(xué)第二次模擬考試.files/image319.gif) 的法向量,所以
的法向量,所以學(xué)第二次模擬考試.files/image385.gif) 與
與學(xué)第二次模擬考試.files/image078.gif) 互余.
互余.
學(xué)第二次模擬考試.files/image395.gif) ,
,學(xué)第二次模擬考試.files/image397.gif) ,
,
所以,直線學(xué)第二次模擬考試.files/image325.gif) 與平面
與平面學(xué)第二次模擬考試.files/image319.gif) 所成角的正弦值為
所成角的正弦值為學(xué)第二次模擬考試.files/image332.gif) .………………………14分
.………………………14分
19.解:(Ⅰ)學(xué)第二次模擬考試.files/image402.gif) ,
,
因?yàn)楹瘮?shù)學(xué)第二次模擬考試.files/image094.gif) 在
在學(xué)第二次模擬考試.files/image180.gif) 及
及學(xué)第二次模擬考試.files/image182.gif) 取得極值,則有
取得極值,則有學(xué)第二次模擬考試.files/image407.gif) ,
,學(xué)第二次模擬考試.files/image409.gif) .
.
即學(xué)第二次模擬考試.files/image411.gif)
解得學(xué)第二次模擬考試.files/image413.gif) ,
,學(xué)第二次模擬考試.files/image415.gif) .………………………7分
.………………………7分
(Ⅱ)由(Ⅰ)可知,學(xué)第二次模擬考試.files/image417.gif) ,
,
學(xué)第二次模擬考試.files/image419.gif) .
.
當(dāng)學(xué)第二次模擬考試.files/image421.gif) 時,
時,學(xué)第二次模擬考試.files/image423.gif) ;
;
當(dāng)學(xué)第二次模擬考試.files/image425.gif) 時,
時,學(xué)第二次模擬考試.files/image427.gif) ;
;
當(dāng)學(xué)第二次模擬考試.files/image429.gif) 時,
時,學(xué)第二次模擬考試.files/image423.gif) .
.
所以,當(dāng)學(xué)第二次模擬考試.files/image180.gif) 時,
時,學(xué)第二次模擬考試.files/image094.gif) 取得極大值
取得極大值學(xué)第二次模擬考試.files/image434.gif) ,又
,又學(xué)第二次模擬考試.files/image436.gif) ,
,學(xué)第二次模擬考試.files/image438.gif) .
.
則當(dāng)學(xué)第二次模擬考試.files/image440.gif) 時,
時,學(xué)第二次模擬考試.files/image094.gif) 的最大值為
的最大值為學(xué)第二次模擬考試.files/image438.gif) .
.
因?yàn)閷τ谌我獾?sub>學(xué)第二次模擬考試.files/image440.gif) ,有
,有學(xué)第二次模擬考試.files/image186.gif) 恒成立,
恒成立,
所以 學(xué)第二次模擬考試.files/image446.gif) ,
,
解得 學(xué)第二次模擬考試.files/image448.gif) 或
或學(xué)第二次模擬考試.files/image450.gif) ,
,
因此學(xué)第二次模擬考試.files/image452.gif) 的取值范圍為
的取值范圍為學(xué)第二次模擬考試.files/image454.gif) .………………………14分
.………………………14分
20.解:(Ⅰ)設(shè)學(xué)第二次模擬考試.files/image112.gif) 的公差為
的公差為學(xué)第二次模擬考試.files/image457.gif) ,
,學(xué)第二次模擬考試.files/image459.gif) 的公比為
的公比為學(xué)第二次模擬考試.files/image461.gif) ,則依題意有
,則依題意有學(xué)第二次模擬考試.files/image463.gif) 且
且學(xué)第二次模擬考試.files/image465.gif)
解得學(xué)第二次模擬考試.files/image467.gif) ,
,學(xué)第二次模擬考試.files/image469.gif) .
.
所以學(xué)第二次模擬考試.files/image471.gif) ,
,
學(xué)第二次模擬考試.files/image473.gif) .………………………6分
.………………………6分
(Ⅱ)學(xué)第二次模擬考試.files/image475.gif) .
.
學(xué)第二次模擬考試.files/image477.gif) ,①
,①
學(xué)第二次模擬考試.files/image479.gif) ,②
,②
②-①得學(xué)第二次模擬考試.files/image481.gif) ,
,
學(xué)第二次模擬考試.files/image483.gif)
學(xué)第二次模擬考試.files/image485.gif)
學(xué)第二次模擬考試.files/image487.gif) .………………………12分
.………………………12分
學(xué)第二次模擬考試.files/image498.gif) 21.證明:(Ⅰ)橢圓的半焦距
21.證明:(Ⅰ)橢圓的半焦距學(xué)第二次模擬考試.files/image500.gif) ,
,
由學(xué)第二次模擬考試.files/image502.gif) 知點(diǎn)
知點(diǎn)學(xué)第二次模擬考試.files/image504.gif) 在以線段
在以線段學(xué)第二次模擬考試.files/image506.gif) 為直徑的圓上,
為直徑的圓上,
故學(xué)第二次模擬考試.files/image508.gif) ,
,
所以,學(xué)第二次模擬考試.files/image510.gif) .………………………6分
.………………………6分
(Ⅱ)(?)當(dāng)學(xué)第二次模擬考試.files/image512.gif) 的斜率
的斜率學(xué)第二次模擬考試.files/image514.gif) 存在且
存在且學(xué)第二次模擬考試.files/image516.gif) 時,
時,學(xué)第二次模擬考試.files/image512.gif) 的方程為
的方程為學(xué)第二次模擬考試.files/image519.gif) ,代入橢圓方程
,代入橢圓方程學(xué)第二次模擬考試.files/image202.gif) ,并化簡得
,并化簡得學(xué)第二次模擬考試.files/image522.gif) .
.
設(shè)學(xué)第二次模擬考試.files/image524.gif) ,
,學(xué)第二次模擬考試.files/image526.gif) ,則
,則
學(xué)第二次模擬考試.files/image528.gif) ,
,學(xué)第二次模擬考試.files/image530.gif) ,
,
學(xué)第二次模擬考試.files/image532.gif) ;
;
因?yàn)?sub>學(xué)第二次模擬考試.files/image534.gif) 與
與學(xué)第二次模擬考試.files/image536.gif) 相交于點(diǎn)
相交于點(diǎn)學(xué)第二次模擬考試.files/image538.gif) ,且
,且學(xué)第二次模擬考試.files/image534.gif) 的斜率為
的斜率為學(xué)第二次模擬考試.files/image541.gif) .
.
所以,學(xué)第二次模擬考試.files/image543.gif) .
.
四邊形學(xué)第二次模擬考試.files/image281.gif) 的面積
的面積
學(xué)第二次模擬考試.files/image546.gif) .
.
當(dāng)學(xué)第二次模擬考試.files/image548.gif) 時,上式取等號.………………………10分
時,上式取等號.………………………10分
(?)當(dāng)學(xué)第二次模擬考試.files/image512.gif) 的斜率
的斜率學(xué)第二次模擬考試.files/image551.gif) 或斜率不存在時,四邊形
或斜率不存在時,四邊形學(xué)第二次模擬考試.files/image281.gif) 的面積
的面積學(xué)第二次模擬考試.files/image554.gif) .……………………11分
.……………………11分
綜上,四邊形學(xué)第二次模擬考試.files/image281.gif) 的面積的最小值為
的面積的最小值為學(xué)第二次模擬考試.files/image557.gif) .………………………12分
.………………………12分
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com