
題目列表(包括答案和解析)
已知 是等差數(shù)列,其前n項(xiàng)和為Sn,
是等差數(shù)列,其前n項(xiàng)和為Sn, 是等比數(shù)列,且
是等比數(shù)列,且 ,
, .
.
(Ⅰ)求數(shù)列 與
與 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ)記 ,
, ,證明
,證明 (
( ).
).
【解析】(1)設(shè)等差數(shù)列 的公差為d,等比數(shù)列
的公差為d,等比數(shù)列 的公比為q.
的公比為q.
由 ,得
,得 ,
, ,
, .
.
由條件,得方程組 ,解得
,解得
所以 ,
, ,
, .
.
(2)證明:(方法一)
由(1)得
 ①
①
 ②
②
由②-①得



而
故 ,
,
(方法二:數(shù)學(xué)歸納法)
① 當(dāng)n=1時(shí),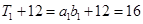 ,
, ,故等式成立.
,故等式成立.
② 假設(shè)當(dāng)n=k時(shí)等式成立,即 ,則當(dāng)n=k+1時(shí),有:
,則當(dāng)n=k+1時(shí),有:






即 ,因此n=k+1時(shí)等式也成立
,因此n=k+1時(shí)等式也成立
由①和②,可知對(duì)任意 ,
, 成立.
成立.
如圖, 是△
是△ 的重心,
的重心, 、
、 分別是邊
分別是邊 、
、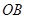 上的動(dòng)點(diǎn),且
上的動(dòng)點(diǎn),且 、
、 、
、 三點(diǎn)共線.
三點(diǎn)共線.
(1)設(shè)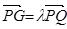 ,將
,將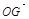 用
用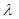 、
、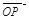 、
、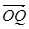 表示;
表示;
(2)設(shè)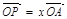 ,
,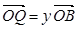 ,證明:
,證明: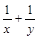 是定值;
是定值;
(3)記△ 與△
與△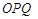 的面積分別為
的面積分別為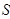 、
、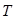 .求
.求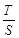 的取值范圍.
的取值范圍.
(提示: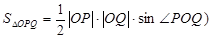
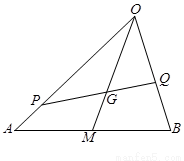
【解析】第一問中利用(1)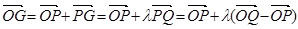
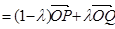
第二問中,由(1),得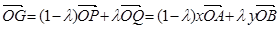 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴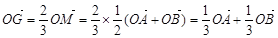
而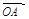 、
、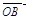 不共線,∴由①、②,得
不共線,∴由①、②,得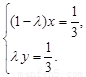
第三問中,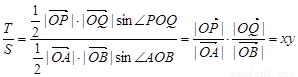
由點(diǎn) 、
、 的定義知
的定義知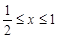 ,
,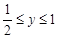 ,
,
且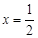 時(shí),
時(shí),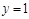 ;
;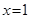 時(shí),
時(shí),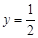 .此時(shí),均有
.此時(shí),均有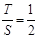 .
.
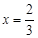 時(shí),
時(shí),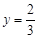 .此時(shí),均有
.此時(shí),均有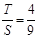 .
.
以下證明: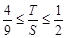 ,結(jié)合作差法得到。
,結(jié)合作差法得到。
解:(1)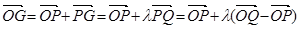
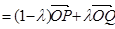 .
.
(2)一方面,由(1),得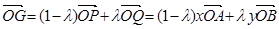 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴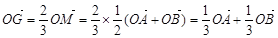 . ②
. ②
而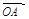 、
、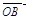 不共線,∴由①、②,得
不共線,∴由①、②,得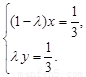
解之,得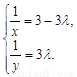 ,∴
,∴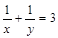 (定值).
(定值).
(3)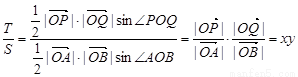 .
.
由點(diǎn) 、
、 的定義知
的定義知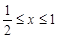 ,
,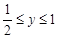 ,
,
且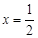 時(shí),
時(shí),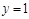 ;
;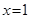 時(shí),
時(shí),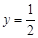 .此時(shí),均有
.此時(shí),均有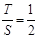 .
.
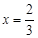 時(shí),
時(shí),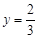 .此時(shí),均有
.此時(shí),均有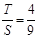 .
.
以下證明: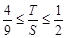 .(法一)由(2)知
.(法一)由(2)知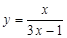 ,
,
∵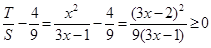 ,∴
,∴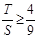 .
.
∵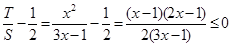 ,∴
,∴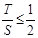 .
.
∴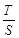 的取值范圍
的取值范圍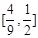
| HM |
| HN |
| 16 |
| 3 |
(1)選其中1人為總負(fù)責(zé)人,有多少種不同的選法?
(2)每一年級(jí)各選1名組長,有多少種不同的選法?
(3)推選出其中2人去外校參觀學(xué)習(xí),要求這2人來自不同年級(jí),有多少種不同的選法?
 ,求雙曲線方程.
,求雙曲線方程.湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com