
題目列表(包括答案和解析)
實際問題:某學校共有18個教學班,每班的學生數都是40人.為了解學生課余時間上網情況,學校打算做一次抽樣調查,如果要確保全校抽取出來的學生中至少有10人在同一班級,那么全校最少需抽取多少名學生?
建立模型:為解決上面的“實際問題”,我們先建立并研究下面從口袋中摸球的數學模型:
在不透明的口袋中裝有紅、黃、白三種顏色的小球各20個(除顏色外完全相同),現要確保從口袋中隨機摸出的小球至少有10個是同色的,則最少需摸出多少個小球?
為了找到解決問題的辦法,我們可把上述問題簡單化:
(1)我們首先考慮最簡單的情況:即要確保從口袋中摸出的小球至少有2個是同色的,則最少需摸出多少個小球?
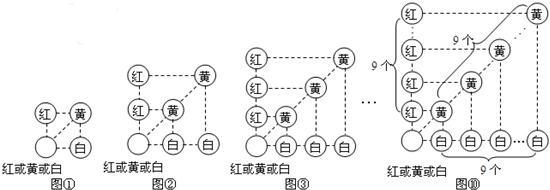
假若從袋中隨機摸出3個小球,它們的顏色可能會出現多種情況,其中最不利的情況就是它們的顏色各不相同,那么只需再從袋中摸出1個小球就可確保至少有2個小球同色,即最少需摸出小球的個數是:1+3=4(如圖①);
(2)若要確保從口袋中摸出的小球至少有3個是同色的呢?
我們只需在(1)的基礎上,再從袋中摸出3個小球,就可確保至少有3個小球同色,即最少需摸出小球的個數是:1+3×2=7(如圖②)
(3)若要確保從口袋中摸出的小球至少有4個是同色的呢?
我們只需在(2)的基礎上,再從袋中摸出3個小球,就可確保至少有4個小球同色,即最少需摸出小球的個數是:1+3×3=10(如圖③):
……
(10)若要確保從口袋中摸出的小球至少有10個是同色的呢?
我們只需在(9)的基礎上,再從袋中摸出3個小球,就可確保至少有10個小球同色,即最少需摸出小球的個數是:1+3×(10-1)=28(如圖⑩)

模型拓展一:在不透明的口袋中裝有紅、黃、白、藍、綠五種顏色的小球各20個(除顏色外完全相同),現從袋中隨機摸球:
(1)若要確保摸出的小球至少有2個同色,則最少需摸出小球的個數是________;
(2)若要確保摸出的小球至少有10個同色,則最少需摸出小球的個數是________;
(3)若要確保摸出的小球至少有n個同色(n<20),則最少需摸出小球的個數是________.
模型拓展二:在不透明口袋中裝有m種顏色的小球各20個(除顏色外完全相同),現從袋中隨機摸球:
(1)若要確保摸出的小球至少有2個同色,則最少需摸出小球的個數是________.
(2)若要確保摸出的小球至少有n個同色(n<20),則最少需摸出小球的個數是________.
問題解決:(1)請把本題中的“實際問題”轉化為一個從口袋中摸球的數學模型;
(2)根據(1)中建立的數學模型,求出全校最少需抽取多少名學生.
實際問題:某學校共有18個教學班,每班的學生數都是40人.為了解學生課余時間上網情況,學校打算做一次抽樣調查,如果要確保全校抽取出來的學生中至少有10人在同一班級,那么全校最少需抽取多少名學生?
建立模型:為解決上面的“實際問題”,我們先建立并研究下面從口袋中摸球的數學模型:
在不透明的口袋中裝有紅、黃、白三種顏色的小球各20個(除顏色外完全相同),現要確保從口袋中隨機摸出的小球至少有10個是同色的,則最少需摸出多少個小球?
為了找到解決問題的辦法,我們可把上述問題簡單化:
(1)我們首先考慮最簡單的情況:即要確保從口袋中摸出的小球至少有2個是同色的,則最少需摸出多少個小球?
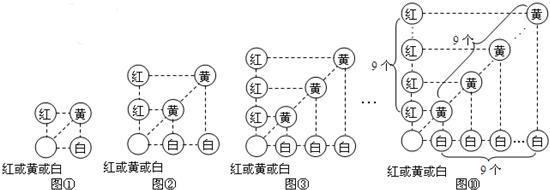
假若從袋中隨機摸出3個小球,它們的顏色可能會出現多種情況,其中最不利的情況就是它們的顏色各不相同,那么只需再從袋中摸出1個小球就可確保至少有2個小球同色,即最少需摸出小球的個數是:![]() (如圖①);
(如圖①);
(2)若要確保從口袋中摸出的小球至少有3個是同色的呢?
我們只需在(1)的基礎上,再從袋中摸出3個小球,就可確保至少有3個小球同色,即最少需摸出小球的個數是:![]() (如圖②)
(如圖②)
(3)若要確保從口袋中摸出的小球至少有4個是同色的呢?
我們只需在(2)的基礎上,再從袋中摸出3個小球,就可確保至少有4個小球同色,即最少需摸出小球的個數是:![]() (如圖③):
(如圖③):
![]()
(10)若要確保從口袋中摸出的小球至少有10個是同色的呢?
我們只需在(9)的基礎上,再從袋中摸出3個小球,就可確保至少有10個小球同色,即最少需摸出小球的個數是:![]() (如圖⑩)
(如圖⑩)

模型拓展一:在不透明的口袋中裝有紅、黃、白、藍、綠五種顏色的小球各20分(除顏色外完全相同),現從袋中隨機摸球:
(1)若要確保摸出的小球至少有2個同色,則最少需摸出小球的個數是 ;
(2)若要確保摸出的小球至少有10個同色,則最少需摸出小球的個數是 ;
(3)若要確保摸出的小球至少有![]() 個同色(
個同色(![]() ),則最少需摸出小球的個數是 .
),則最少需摸出小球的個數是 .
模型拓展二:在不透明口袋中裝有![]() 種顏色的小球各20個(除顏色外完全相同),現從袋中隨機摸球:
種顏色的小球各20個(除顏色外完全相同),現從袋中隨機摸球:
(1)若要確保摸出的小球至少有2個同色,則最少需摸出小球的個數是 .
(2)若要確保摸出的小球至少有![]() 個同色(
個同色(![]() ),則最少需摸出小球的個數是 .
),則最少需摸出小球的個數是 .
問題解決:(1)請把本題中的“實際問題”轉化為一個從口袋中摸球的數學模型;
(2)根據(1)中建立的數學模型,求出全校最少需抽取多少名學生.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com