
題目列表(包括答案和解析)
| 2 |

 (2013•石景山區一模)如圖,把兩個全等的Rt△AOB和Rt△ECD分別置于平面直角坐標系xOy中,使點E與點B重合,直角邊OB、BC在y軸上.已知點D (4,2),過A、D兩點的直線交y軸于點F.若△ECD沿DA方向以每秒
(2013•石景山區一模)如圖,把兩個全等的Rt△AOB和Rt△ECD分別置于平面直角坐標系xOy中,使點E與點B重合,直角邊OB、BC在y軸上.已知點D (4,2),過A、D兩點的直線交y軸于點F.若△ECD沿DA方向以每秒| 2 |
 我國古代數學家趙爽的“勾股圓方圖”是由四個全等的直角三角形與中間的一個小正方形拼成一個大正方形(如圖所示).如果大正方形的面積是49,小正方形的面積4,直角三角形的兩直角邊長分別為a,b,那么下列結論正確的有( )個.
我國古代數學家趙爽的“勾股圓方圖”是由四個全等的直角三角形與中間的一個小正方形拼成一個大正方形(如圖所示).如果大正方形的面積是49,小正方形的面積4,直角三角形的兩直角邊長分別為a,b,那么下列結論正確的有( )個.| 94 |
| 94 |
| A.1個 | B.2個 | C.3個 | D.4個 |

 我國古代數學家趙爽的“勾股圓方圖”是由四個全等的直角三角形與中間的一個小正方形拼成一個大正方形(如圖所示).如果大正方形的面積是49,小正方形的面積4,直角三角形的兩直角邊長分別為a,b,那么下列結論正確的有____個.
我國古代數學家趙爽的“勾股圓方圖”是由四個全等的直角三角形與中間的一個小正方形拼成一個大正方形(如圖所示).如果大正方形的面積是49,小正方形的面積4,直角三角形的兩直角邊長分別為a,b,那么下列結論正確的有____個.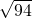 .
.湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com