日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

閱讀材料：多邊形的頂點、邊上或內部的一點與多邊形各頂點的連線，能夠將多邊形分割成若干個小三角形。如圖給出了四邊形的具體分割方法，分別將四邊形分割成2個、3個、4個小三角形，可以得到四邊形的內角和為360°。

（1）請你按照上述方法將圖中的五邊形進行分割，并寫出得到的小三角形的個數；

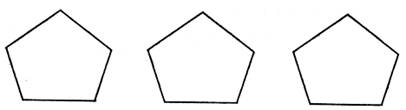
分別分割成            、           、           個小三角形；

（2）試把這一結論推廣至邊形，分別寫出按照上述三種分割方法得到的小三角形的個數（按規律寫出結論即可，可以不畫圖），并根據其中的一種分割方法推導出邊形的內角和（畫出示意圖）。

邊形：分割成           、           、           個小三角形。試推導邊形的內角和。

問題提出
我們在分析解決某些數學問題時，經常要比較兩個數或代數式的大小，而解決問題的策略一般要進行一定的轉化，其中“作差法”就是常用的方法之一．所謂“作差法”：就是通過作差、變形，并利用差的符號確定他們的大小，即要比較代數式M、N的大小，只要作出它們的差M－N，若M－N＞0，則M＞N；若M－N＝0，則M＝N；若M－N＜0，則M＜N．
問題解決
如圖1，把邊長為a＋b(a≠b)的大正方形分割成兩個邊長分別是a、b的小正方形及兩個矩形，試比較兩個小正方形面積之和M與兩個矩形面積之和N的大小．

解：由圖可知：M＝a²＋b²，N＝2ab．
∴M－N＝a²＋b²－2ab＝(a－b)²．
∵a≠b，∴(a－b)²＞0．
∴M－N＞0．
∴M＞N．
類比應用
【小題1】已知：多項式M ＝2a²－a＋1 ，N ＝a²－2a．試比較M與N的大小．
【小題2】已知：如圖，銳角△ABC (其中BC為a，AC為b，AB為c)三邊
滿足a ＜b ＜ c ，現將△ABC 補成長方形，使得△ABC的兩個頂
點為長方形的兩個端點，第三個頂點落在長方形的這一邊的對邊上。                     
①這樣的長方形可以畫       個；
②所畫的長方形中哪個周長最小？為什么？

拓展延伸                                                                                               
已知：如圖，銳角△ABC (其中BC為a，AC為b，AB為c)三邊滿足a ＜b ＜ c ，畫其BC邊上的內接正方形EFGH , 使E、F兩點在邊BC上，G、H分別在邊AC、AB上，同樣還可畫AC、AB邊上的內接正方形，問哪條邊上的內接正方形面積最大？為什么？

【問題提出】我們在分析解決某些數學問題時，經常要比較兩個數或代數式的大小，而解決問題的策略一般要進行一定的轉化，其中“作差法”就是常用的方法之一．所謂“作差法”：就是通過作差、變形，并利用差的符號確定他們的大小，即要比較代數式M、N的大小，只要作出它們的差M－N，若M－N＞0，則M＞N；若M－N＝0，則M＝N；若M－N＜0，則M＜N．
【問題解決】如圖1，把邊長為a＋b(a≠b)的大正方形分割成兩個邊長分別是a、b的小正方形及兩個矩形，試比較兩個小正方形面積之和M與兩個矩形面積之和N的大小．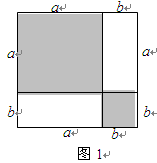

解：由圖可知：，．
∴．
∵a≠b，∴＞0．
∴M－N＞0．∴M＞N．
【類比應用】(1)已知：多項式M ＝2a²－a＋1 ，N ＝a²－2a ．
試比較M與N的大小．
(2)已知：如圖2，銳角△ABC (其中BC為a ，AC為 b，
AB為c)三邊滿足a ＜b ＜ c ，現將△ABC 補成長方形，
使得△ABC的兩個頂點為長方形的兩個端點，第三個頂點落
在長方形的這一邊的對邊上。
 
①這樣的長方形可以畫     個；
②所畫的長方形中哪個周長最小？為什么？
【拓展延伸】 已知：如圖，銳角△ABC (其中BC為a，AC為b，AB為c)三邊滿足a ＜b ＜ c ，畫其BC邊上的內接正方形EFGH , 使E、F兩點在邊BC上，G、H分別在邊AC、AB上，同樣還可畫AC、AB邊上的內接正方形，問哪條邊上的內接正方形面積最大？為什么？

【問題提出】我們在分析解決某些數學問題時，經常要比較兩個數或代數式的大小，而解決問題的策略一般要進行一定的轉化，其中“作差法”就是常用的方法之一．所謂“作差法”：就是通過作差、變形，并利用差的符號確定他們的大小，即要比較代數式M、N的大小，只要作出它們的差M－N，若M－N＞0，則M＞N；若M－N＝0，則M＝N；若M－N＜0，則M＜N．

【問題解決】如圖1，把邊長為a＋b(a≠b)的大正方形分割成兩個邊長分別是a、b的小正方形及兩個矩形，試比較兩個小正方形面積之和M與兩個矩形面積之和N的大小．

解：由圖可知：，．

∴．

∵a≠b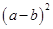，∴＞0．

∴M－N＞0．∴M＞N．

【類比應用】(1)已知：多項式M ＝2a²－a＋1 ，N ＝a²－2a ．

試比較M與N的大小．

(2)已知：如圖2，銳角△ABC (其中BC為a ，AC為 b，

AB為c)三邊滿足a ＜b ＜ c ，現將△ABC 補成長方形，

使得△ABC的兩個頂點為長方形的兩個端點，第三個頂點落

在長方形的這一邊的對邊上。

①這樣的長方形可以畫     個；

②所畫的長方形中哪個周長最小？為什么？

【拓展延伸】 已知：如圖，銳角△ABC (其中BC為a，AC為b，AB為c)三邊滿足a ＜b ＜ c ，畫其BC邊上的內接正方形EFGH , 使E、F兩點在邊BC上，G、H分別在邊AC、AB上，同樣還可畫AC、AB邊上的內接正方形，問哪條邊上的內接正方形面積最大？為什么？