(1)已知,如圖(1)所示,△ABC中,D、E分別是邊AB、AC上的中點,連結DE。試說明DE與BC的關系。
解:DE與BC的關系為DE∥BC且DE=

BC。
理由如下:
將△ADE繞點D旋轉180°到△BDF位置
根據旋轉的特征,有F、D、E三點在同一直線上
∴DF=DE,BF=AE,且BF∥AE,
∴∠1=∠A,∠F=∠2
∵AE=EC
∴BF=EC
由于一組對邊平行且相等的四邊形為平行四邊形
∴四邊形FBCE是平行四邊形
∴FE∥BC且FE=BC
即DE∥BC,DE=
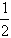
BC。
(2)已知:如圖(2)所示,在梯形ABCD中,AD∥BC,E、F分別是AB、CD的中點,連結EF,試問你能根據(1)題的結論,說明EF∥BC,且EF=

(AD+BC)嗎?



 BC。
BC。 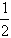 BC。
BC。 (AD+BC)嗎?
(AD+BC)嗎?