
題目列表(包括答案和解析)
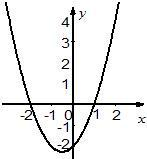 24、拋物線與坐標軸交點如圖所示,一次函數y=k(x-2)的圖象與該拋物線相切(即只有一個交點).
24、拋物線與坐標軸交點如圖所示,一次函數y=k(x-2)的圖象與該拋物線相切(即只有一個交點).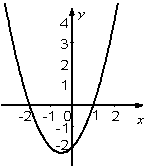
 個單位長度,再向上平移
個單位長度,再向上平移 個單位長度,隨著k的變化,平移后的拋物線的頂點都在某個新函數的圖象上,求新函數的解析式(不要求寫自變量的取值范圍).
個單位長度,隨著k的變化,平移后的拋物線的頂點都在某個新函數的圖象上,求新函數的解析式(不要求寫自變量的取值范圍). ,縱坐標增大
,縱坐標增大 分別作為點A的橫、縱坐標;把頂點的橫坐標增加
分別作為點A的橫、縱坐標;把頂點的橫坐標增加 ,縱坐標增加
,縱坐標增加 分別作為點B的橫、縱坐標,則A,B兩點也在拋物線y=ax2+2x+3(a≠0)上.
分別作為點B的橫、縱坐標,則A,B兩點也在拋物線y=ax2+2x+3(a≠0)上. ,縱坐標增大
,縱坐標增大 分別作為點A的橫、縱坐標;把頂點的橫坐標增加
分別作為點A的橫、縱坐標;把頂點的橫坐標增加 ,縱坐標增加
,縱坐標增加 分別作為點B的橫、縱坐標,則A,B兩點也在拋物線y=ax2+2x+3(a≠0)上。
分別作為點B的橫、縱坐標,則A,B兩點也在拋物線y=ax2+2x+3(a≠0)上。湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com