
題目列表(包括答案和解析)
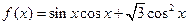
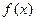 的最小正周期;
的最小正周期;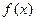 在區間
在區間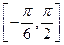 上的最大值和最小值
上的最大值和最小值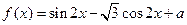
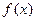 的最小正周期和單調增區間;
的最小正周期和單調增區間;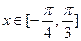 時,函數
時,函數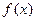 的最大值與最小值的和
的最大值與最小值的和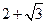 ,求
,求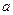
已知![]() .
.
(Ⅰ)求![]() 的最小正周期;
的最小正周期;
(Ⅱ)當![]() 為何值時,
為何值時,![]() 取得最大值,最大值是多少?
取得最大值,最大值是多少?
(Ⅲ)求![]() 的單調遞減區間.
的單調遞減區間.
最小正周期為π的函數![]() (其中a是小于零的常數,
(其中a是小于零的常數,![]() 是大于零的常數)的圖象按向量
是大于零的常數)的圖象按向量![]() ,(0<θ<π)平移后得到函數y=f(x)的圖象,而函數y=f(x)在實數集上的值域為[-2,2],且在區間
,(0<θ<π)平移后得到函數y=f(x)的圖象,而函數y=f(x)在實數集上的值域為[-2,2],且在區間![]() 上是單調遞減函數.
上是單調遞減函數.
(1)求a、![]() 和θ的值;
和θ的值;
(2)若角α和β的終邊不共線,f(α)+g(α)=f(β)+g(β),求tan(α+β)的值.
函數![]() 的最小正周期為
的最小正周期為![]() ,
,
(Ⅰ)求![]() 的單調遞增區間;
的單調遞增區間;
(Ⅱ)在![]() 中,角A,B,C的對邊分別是
中,角A,B,C的對邊分別是![]() ,且滿足
,且滿足![]() ,
,
求角B的值,并求函數![]() 的取值范圍.
的取值范圍.
一、選擇題(5分×12=60分)
B B D D C B B D D C A A
二、填空題(4分x 4=16分)
13.80 14.32 15. 16.①③
16.①③
三、解答題(12分×5+14分=74分)
17.解:(1) 2分
2分
 ……………………4分
……………………4分
 ∴
∴ 的最小正周期為
的最小正周期為 …………………6分
…………………6分
(2)∵ 成等比數列 ∴
成等比數列 ∴ 又
又
∴ ……………………………………4分
……………………………………4分
又∵ ∴
∴ ……………………………………………………10分
……………………………………………………10分
 ……………………………………12分
……………………………………12分
18.解:(1)設 公差
公差 由
由 成等比數列得
成等比數列得 …………………1分
…………………1分
∴即 ∴
∴ 舍去或
舍去或 …………………………3分
…………………………3分
∴ ………………………………………………4分
………………………………………………4分
∴ ………………………………………………6分
………………………………………………6分
(2) ∵ ………………………………………………7分
………………………………………………7分
∴ …①
…………8分
…①
…………8分
 …………②
…………9分
…………②
…………9分
①-②得:

∴ ………………………………………………12分
………………………………………………12分
19.解:(1)記“任取2張卡片,將卡片上的函數相加得到偶函數”為事件A,
 ……………………………………………………4分
……………………………………………………4分
(2)設符合題設條件,抽取次數恰為3的事件記為B,則
 ………………………………………………12分
………………………………………………12分
20.解:(1)連結

 為正△
…1分
為正△
…1分






 面
面
 3分
3分
面 面
面



即點 的位置在線段
的位置在線段 的四等分點且靠近
的四等分點且靠近 處 ………………………………………6分
處 ………………………………………6分
(2)過 作
作 于
于 ,連
,連
 由(1)知
由(1)知 面
面 (三垂線定理)
(三垂線定理)
∴ 為二面角
為二面角 的平面角……9分
的平面角……9分




在 中,
中,
在 中,
中,
∴二面角 的大小為
的大小為 ………………………………………12分
………………………………………12分
(說明:若用空間向量解,請參照給分)
21.解:(1) 由
由 得
得 ……2分
……2分
①當 時,
時, 在
在 內是增函數,故無最小值………………………3分
內是增函數,故無最小值………………………3分
 ②當
②當 時,
時,
 在
在 處取得極小值
處取得極小值 ………………………5分
………………………5分


由
解得: ≤
≤ ∴
∴ ≤
≤
 …………6分
…………6分
 ≥
≥
(2)由(1)知 在區間
在區間 上均為增函數
上均為增函數
又 ,故要在
,故要在 內
內 為增函數
為增函數


 ≤
≤
 ≥
≥
必須: 或 ………………………………………10分
 ≤
≤
 ≤
≤
 ∴
∴ ≤
≤ 或
或 ≥
≥ ∴實數
∴實數 的取值范圍是:
的取值范圍是: …………………12分
…………………12分
22.解:(1)如圖,設 為橢圓的下焦點,連結
為橢圓的下焦點,連結
∴ ∵
∵ ∴
∴ …3分
…3分
∵ ∴
∴ ………4分
………4分
∴ 的離心率為
的離心率為
…………………………………………………………6分
(2)∵ ,∴拋物線方程為:
,∴拋物線方程為: 設點
設點 則
則 ∵
∵
∴ 點處拋物線
點處拋物線 的切線斜率
的切線斜率 ……………………………………………………8分
……………………………………………………8分
則切線 方程為:
方程為: ……………………………………………………9分
……………………………………………………9分
又∵過點 ∴
∴ ∴
∴ ∴
∴
代入橢圓 方程得:
方程得: ……………………………………………………11分
……………………………………………………11分
∴ ≥
≥ ………………13分
………………13分




當且僅當 即 上式取等號


∴此時橢圓的方程為: ………………………………………………14分
………………………………………………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com