
題目列表(包括答案和解析)
造船廠年造船量20艘,造船![]() 艘產值函數為
艘產值函數為![]() (單位:萬元),成本函數
(單位:萬元),成本函數![]() (單位:萬元),又在經濟學中,函數
(單位:萬元),又在經濟學中,函數![]() 的邊際函數
的邊際函數![]() 定義為
定義為![]()
(1)求利潤函數![]() 及邊際利潤函數
及邊際利潤函數![]() (利潤=產值—成本)
(利潤=產值—成本)
(2)問年造船量安排多少艘時,公司造船利潤最大
(3)邊際利潤函數![]()
![]() 的單調遞減區間
的單調遞減區間
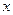 艘產值函數為
艘產值函數為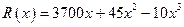 (單位:萬元),成本函數
(單位:萬元),成本函數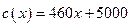 (單位:萬元),又在經濟學中,函數
(單位:萬元),又在經濟學中,函數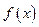 的邊際函數
的邊際函數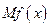 定義為
定義為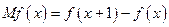
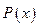 及邊際利潤函數
及邊際利潤函數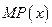 (利潤=產值—成本)
(利潤=產值—成本)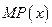
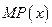 的單調遞減區間
的單調遞減區間某造船公司年最高造船量是20艘. 已知造船x艘的產值函數R (x)=3700x + 45x2 – 10x3(單位:萬元), 成本函數為C (x) = 460x + 5000 (單位:萬元). 又在經濟學中,函數f(x)的邊際函數Mf (x)定義為: Mf (x) = f (x+1) – f (x). 求:(提示:利潤 = 產值 – 成本)
(1) 利潤函數P(x) 及邊際利潤函數MP(x);
(2) 年造船量安排多少艘時, 可使公司造船的年利潤最大?
(3) 邊際利潤函數MP(x)的單調遞減區間, 并說明單調遞減在本題中的實際意義是什么?
一、選擇題(每題5分,共60分)
1―5 ACCBA 6―10 BCABD 11―12 DB
|