
題目列表(包括答案和解析)
【必做題】第22題和第23題為必做題, 每小題10分,共20分.要寫出必要的文字說明或演算步驟.
有甲、乙兩個箱子,甲箱 中有
中有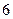 張卡片,其中
張卡片,其中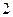 張寫有數字
張寫有數字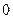 ,
,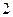 張寫有數字
張寫有數字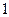 ,
,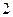 張寫有數字
張寫有數字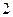 ;乙箱中也有
;乙箱中也有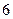 張卡片,其中
張卡片,其中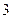 張寫有數
張寫有數 字
字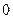 ,
,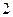 張寫有數字
張寫有數字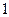 ,
,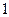 張寫有數字
張寫有數字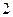 .
.
(1)如果從甲、乙箱中各取一張卡片,設取出的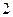 張卡片上數字之積為
張卡片上數字之積為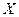 ,求
,求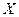 的
的
分布列及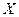 的
的 數學期望;
數學期望;
(2)如果從甲箱中取一張卡片,從乙箱中取兩張卡片,那么取出的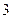 張卡片都寫有
張卡片都寫有
數字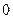 的概率是多少?
的概率是多少?
【必做題】第22題和第23題為必做題, 每小題10分,共20分.要寫出必要的文字說明或演算步驟.
有甲、乙兩個箱子,甲箱中有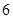 張卡片,其中
張卡片,其中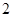 張寫有數字
張寫有數字 ,
,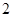 張寫有數字
張寫有數字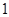 ,
,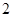 張寫有數字
張寫有數字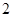 ;乙箱中也有
;乙箱中也有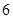 張卡片,其中
張卡片,其中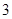 張寫有數字
張寫有數字 ,
,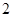 張寫有數字
張寫有數字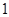 ,
,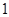 張寫有數字
張寫有數字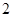 .
.
(1)如果從甲、乙箱中各取一張卡片,設取出的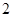 張卡片上數字之積為
張卡片上數字之積為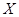 ,求
,求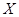 的
的
分布列及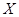 的數學期望;
的數學期望;
(2)如果從甲箱中取一張卡片,從乙箱中取兩張卡片,那么取出的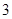 張卡片都寫有
張卡片都寫有
數字 的概率是多少?
的概率是多少?
 中有
中有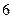 張卡片,其中
張卡片,其中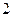 張寫有數字
張寫有數字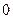 ,
,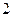 張寫有數字
張寫有數字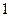 ,
,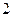 張寫有數字
張寫有數字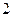 ;乙箱中也有
;乙箱中也有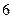 張卡片,其中
張卡片,其中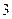 張寫有數
張寫有數 字
字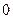 ,
,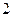 張寫有數字
張寫有數字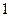 ,
,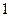 張寫有數字
張寫有數字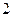 .
.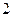 張卡片上數字之積為
張卡片上數字之積為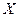 ,求
,求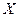 的
的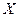 的
的 數學期望;
數學期望;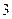 張卡片都寫有
張卡片都寫有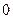 的概率是多少?
的概率是多少?【必做題】第22題、第23題,每題10分,共計20分.請在答題卡指定區域內作答,解答時應寫出
文字說明、證明過程或演算步驟。http://www.mathedu.cn
22. (本小題滿分10分)
如圖,在正四棱柱 中,
中,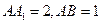 ,點
,點 是
是 的中點,點
的中點,點 在
在 上,設二面角
上,設二面角 的大小為
的大小為 。
。
(1)當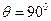 時,求
時,求 的長;
的長;
(2)當 時,求
時,求 的長。
的長。
[選做題]本題包括A、B、C、D四小題,請選定其中兩題,并在相應的答題區域內作答。若多做,則按作答的前兩題評分。解答時應寫出文字說明、證明過程或演算步驟。
A.  選修4-1:幾何證明選講
選修4-1:幾何證明選講
AB是圓O的直徑,D為圓O上一點,過D作圓O的切線交AB延長線于點C,若DA=DC,求證:AB=2BC。
B. 選修4-2:矩陣與變換
在平面直角坐標系xOy中,已知點A(0,0),B(-2,0),C(-2,1)。設k為非零實數,矩陣M= ,N=
,N= ,點A、B、C在矩陣MN對應的變換下得到點分別為A1、B1、C1,△A1B1C1的面積是△ABC面積的2倍,求k的值。
,點A、B、C在矩陣MN對應的變換下得到點分別為A1、B1、C1,△A1B1C1的面積是△ABC面積的2倍,求k的值。
C. 選修4-4:坐標系與參數方程
在極坐標系中,已知圓ρ=2cosθ與直線3ρcosθ+4ρsinθ+a=0相切,求實數a的值。
D. 選修4-5:不等式選講
設a、b是非負實數,求證: 。
。
[必做題]第22題、第23題,每題10分,共計20分。請在答題卡指定區域內作答,解答時應寫出文字說明、證明過程或演算步驟。
一、填空題:(本大題共14小題,每小題5分,共70分.)
1. 2.1 3.-2 4.
2.1 3.-2 4. 5. (1)(2)
5. (1)(2)
6. 4 7.甲 8. 9.9 10.
9.9 10.
11.-2
12. 13.2 14. 2
13.2 14. 2
二、解答題:(本大題共6小題,共90分.)
15.(本小題滿分14分)
解:(1)∵
∴ …………………………………………5分
…………………………………………5分
(2)∵ ∴
∴
…………………………………………7分

 ……………………………………9分
……………………………………9分



 或
或
 或7
………………………………14分
或7
………………………………14分
16.(本小題滿分14分)
(1)證明: E、P分別為AC、A′C的中點,
E、P分別為AC、A′C的中點,
 EP∥A′A,又A′A
EP∥A′A,又A′A 平面AA′B,EP
平面AA′B,EP 平面AA′B
平面AA′B
∴即EP∥平面A′FB …………………………………………5分
(2) 證明:∵BC⊥AC,EF⊥A′E,EF∥BC
∴BC⊥A′E,∴BC⊥平面A′EC
BC 平面A′BC
平面A′BC
∴平面A′BC⊥平面A′EC …………………………………………9分
(3)證明:在△A′EC中,P為A′C的中點,∴EP⊥A′C,
在△A′AC中,EP∥A′A,∴A′A⊥A′C
由(2)知:BC⊥平面A′EC 又A′A 平面A′EC
平面A′EC
∴BC⊥AA′
∴A′A⊥平面A′BC …………………………………………14分
17.(本小題滿分15分)
解:(1)取弦的中點為M,連結OM
由平面幾何知識,OM=1
 …………………………………………3分
…………………………………………3分
解得: ,
, ………………………………………5分
………………………………………5分
∵直線過F、B ,∴ 則
則 …………………………………………6分
…………………………………………6分
(2)設弦的中點為M,連結OM
則
 ……………………………………9分
……………………………………9分
解得 …………………………………………11分
…………………………………………11分

∴ …………………………………………15分
…………………………………………15分
(本題也可以利用特征三角形中的有關數據直接求得)
18.(本小題滿分15分)
(1)延長BD、CE交于A,則AD= ,AE=2
,AE=2
則S△ADE= S△BDE= S△BCE=
∵S△APQ= ,∴
,∴
∴
 …………………………………………7分
…………………………………………7分
(2)

= ?
?
…………………………………………12分
當 ,
,
即 ,
, 
…………………………………………15分
19.(本小題滿分16分)
解(1)證:
 由
由 得
得
在 上點
上點 處的切線為
處的切線為 ,即
,即
又在 上點
上點 處切線可計算得
處切線可計算得 ,即
,即
∴直線 與
與 、
、 都相切,且切于同一點(
都相切,且切于同一點( ) …………………5分
) …………………5分
(2)
 …………………7分
…………………7分
∴ 在
在 上遞增
上遞增
∴當 時
時 ……………10分
……………10分
(3)
設上式為 ,假設
,假設 取正實數,則
取正實數,則 ?
?
當 時,
時, ,
, 遞減;
遞減;
當 ,
, ,
, 遞增. ……………………………………12分
遞增. ……………………………………12分



∴不存在正整數 ,使得
,使得
即 …………………………………………16分
…………………………………………16分
20.(本小題滿分16分)
解:(1) ,
,
 ,
, 對一切
對一切 恒成立
恒成立
 的最小值,又
的最小值,又 ,
,
 …………………………………………4分
…………………………………………4分
(2) 這5個數中成等比且公比
這5個數中成等比且公比 的三數只能為
的三數只能為
 只能是
只能是 ,
,
 …………………………8分
…………………………8分





 ,
, 顯然成立
……………………………………12分
顯然成立
……………………………………12分
當 時,
時, ,
,


 使不等式
使不等式 成立的自然數n恰有4個的正整數p值為3
成立的自然數n恰有4個的正整數p值為3
……………………………………………16分
泰州市2008~2009學年度第二學期期初聯考
高三數學試題參考答案
附加題部分
21.(選做題)(從A,B,C,D四個中選做2個,每題10分,共20分.)
A.解:(1)
∴
∴AB=CD ……………………………………4分
(2)由相交弦定理得
2×1=(3+OP)(3-OP)
∴ ,∴
,∴ ……………………………………10分
……………………………………10分
B.解:依題設有: ………………………………………4分
………………………………………4分
令 ,則
,則 …………………………………………5分
…………………………………………5分
 …………………………………………7分
…………………………………………7分




 ………………………………10分
………………………………10分
C.解:以有點為原點,極軸為 軸正半軸,建立平面直角坐標系,兩坐標系中取相同的長度單位.(1)
軸正半軸,建立平面直角坐標系,兩坐標系中取相同的長度單位.(1) ,
, ,由
,由 得
得 .
.
所以 .
.
即 為圓
為圓 的直角坐標方程. ……………………………………3分
的直角坐標方程. ……………………………………3分
同理 為圓
為圓 的直角坐標方程. ……………………………………6分
的直角坐標方程. ……………………………………6分
(2)由
相減得過交點的直線的直角坐標方程為 . …………………………10分
. …………………………10分
D.證明:(1)因為
所以 …………………………………………4分
…………………………………………4分
(2)∵ …………………………………………6分
…………………………………………6分
同理, ,
, ……………………………………8分
……………………………………8分
三式相加即得 ……………………………10分
……………………………10分
22.(必做題)(本小題滿分10分)
解:(1)記“恰好選到1個曾經參加過數學研究性學習活動的同學”為事件的 , 則其概率為
, 則其概率為 …………………………………………4分
…………………………………………4分
答:恰好選到1個曾經參加過數學研究性學習活動的同學的概率為
(2)隨機變量
 ……………………5分
……………………5分
 …………………………6分
…………………………6分
 ………………………………7分
………………………………7分
∴隨機變量 的分布列為
的分布列為

2
3
4
P



∴ …………………………10分
…………………………10分
23.(必做題)(本小題滿分10分)
(1) ,
, ,
, ,
,
 ,
,
 ……………………………………3分
……………………………………3分
(2)平面BDD1的一個法向量為
設平面BFC1的法向量為
 ∴
∴
取 得平面BFC1的一個法向量
得平面BFC1的一個法向量

∴所求的余弦值為 ……………………………………6分
……………………………………6分
(3)設 (
( )
)
 ,由
,由 得
得
即 ,
,



 當
當 時,
時,
當 時,∴
時,∴ ……………………………………10分
……………………………………10分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com