
題目列表(包括答案和解析)
(本小題滿分14分)如圖,已知三角形PAQ頂點P(-3,0),點A在y軸上,點Q在x軸正半軸上,![]() ·
·![]() =0,
=0, ![]() =2
=2![]() .(1)當(dāng)點A在y軸上移動時,求動點M的軌跡E的方程;
.(1)當(dāng)點A在y軸上移動時,求動點M的軌跡E的方程;
(2)設(shè)直線l:y=k(x+1)與軌跡E交于B、C兩點,點D(1,0),若∠BDC為鈍角,求k的取值范圍.
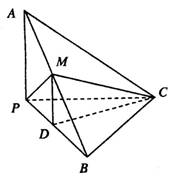
(本小題滿分14分)
如圖,已知三棱錐A—BPC中,AP⊥PC, AC⊥BC,
M為AB中點,D為PB中點,且△PMB為正三角形。
(Ⅰ)求證:DM∥平面APC;
(Ⅱ)求證:平面ABC⊥平面APC;
(Ⅲ)若BC=4,AB=20,求三棱錐D—BCM的體積.
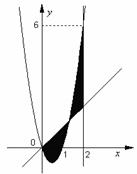
(本小題滿分14分) 如圖,已知二次函數(shù)![]() ,直線
,直線![]() ,直線
,直線![]() (其中
(其中![]() ,
,![]() 為常數(shù));.若直線
為常數(shù));.若直線![]() 的圖象以及
的圖象以及![]() 的圖象所圍成的封閉圖形如陰影所示.
的圖象所圍成的封閉圖形如陰影所示.
(Ⅰ)求![]() ; (Ⅱ)求陰影面積s關(guān)于t的函數(shù)
; (Ⅱ)求陰影面積s關(guān)于t的函數(shù)![]() 的解析式;
的解析式;
(Ⅲ)若過點![]() 可作曲線
可作曲線![]() 的三條切線,求實數(shù)m的取值范圍.
的三條切線,求實數(shù)m的取值范圍.
(本小題滿分14分)
如圖,已知正三棱柱 的底面邊
的底面邊 長是
長是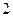 ,
, 是側(cè)棱
是側(cè)棱 的中點,直線
的中點,直線 與側(cè)面
與側(cè)面 所成的角為
所成的角為 .
.
(1)求此正三棱柱的側(cè)棱長;
(2)求二面角 的正切值;
的正切值;
(3)求點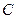 到平面
到平面 的距離.
的距離.
(本小題滿分14分)如圖,已知矩形ABCD的邊AB="2" ,BC= ,點E、F分別是邊AB、CD的中點,沿AF、EC分別把三角形ADF和三角形EBC折起,使得點D和點B重合,記重合后的位置為點P。
,點E、F分別是邊AB、CD的中點,沿AF、EC分別把三角形ADF和三角形EBC折起,使得點D和點B重合,記重合后的位置為點P。
(1)求證:平面PCE 平面PCF;
平面PCF;
(2)設(shè)M、N分別為棱PA、EC的中點,求直線MN與平面PAE所成角的正弦;
(3)求二面角A-PE-C的大小。

1. -學(xué).files/image184.gif) 2.
2. 學(xué).files/image186.gif) 3.
3.
學(xué).files/image188.gif) 4.
4.
學(xué).files/image190.gif)
5. 學(xué).files/image192.gif) 6.
6.
學(xué).files/image194.gif) 或
或學(xué).files/image196.gif) 7. ④
8.
7. ④
8. 學(xué).files/image198.gif)
9. 學(xué).files/image200.gif) 10. (2,4] 11. (28,44) 12.
10. (2,4] 11. (28,44) 12. 學(xué).files/image202.gif)
13. 5 14. m>學(xué).files/image204.gif)
15.(1)【證明】∵△PAB中, D為AB中點,M為PB中點,∴學(xué).files/image206.gif)
∵DM學(xué).files/image208.gif) 平面
平面學(xué).files/image094.gif) ,PA
,PA學(xué).files/image210.gif) 平面
平面學(xué).files/image094.gif) ,∴
,∴學(xué).files/image092.gif) 平面
平面學(xué).files/image094.gif) ……3分
……3分
(2)【證明】∵D是AB的中點,△PDB是正三角形,AB=20,
學(xué).files/image212.gif) ∴
∴學(xué).files/image214.gif) ……4分
……4分
∴△PAB是直角三角形,且AP⊥PB,……5分
又∵AP⊥PC,學(xué).files/image216.gif) ……6分
……6分
∴AP⊥平面PBC.∴AP⊥BC.……8分
又∵AC⊥BC, AP∩AC=A,∴BC⊥平面PAC.……9分
∵學(xué).files/image218.gif) ∴平面PAC⊥平面ABC.……10分
∴平面PAC⊥平面ABC.……10分
(3)【解】由(1)知學(xué).files/image206.gif) ,由(2)知PA⊥平面PBC,
,由(2)知PA⊥平面PBC,
∴DM⊥平面PBC.……11分
∵正三角形PDB中易求得學(xué).files/image221.gif) ,
,
學(xué).files/image223.gif) ……13分
……13分
∴學(xué).files/image225.gif) ……14分
……14分
16.解:(Ⅰ)∵學(xué).files/image227.gif)
學(xué).files/image229.gif) ………………………………………………………………4分
………………………………………………………………4分
又∵學(xué).files/image231.gif) ……………………………………6分
……………………………………6分
即 學(xué).files/image233.gif)
∴ymax=5, ymin=3 …………………………………………………………………8分
(Ⅱ)∵學(xué).files/image235.gif) ……………………………10分
……………………………10分
又∵P為q的充分條件 ∴ 學(xué).files/image237.gif)
學(xué).files/image239.gif) ………………………………………13分
………………………………………13分
解得 3<m<5 ……………………………………………………………………14分
17. 解:(1)由題意知,需加工G型裝置4000個,加工H型裝置3000個,所用工人分別為x人,(216-x)人.
∴g(x)=學(xué).files/image241.gif) ,h(x)=
,h(x)=學(xué).files/image243.gif) ,
,
即g(x)=學(xué).files/image245.gif) ,h(x)=
,h(x)=學(xué).files/image247.gif) (0<x<216,x∈N*). ……………………4分
(0<x<216,x∈N*). ……………………4分
(2)g(x)-h(x)=學(xué).files/image245.gif) -
-學(xué).files/image247.gif) =
=學(xué).files/image249.gif) .
.
∵0<x<216,
∴216-x>0.
當(dāng)0<x≤86時,432-5x>0,g(x)-h(x)>0,g(x)>h(x);
當(dāng)87≤x<216時,432-5x<0,g(x)-h(x)<0,g(x)<h(x).
∴f(x)=學(xué).files/image251.gif) ……………………8分
……………………8分
(3)完成總?cè)蝿?wù)所用時間最少即求f(x)的最小值.
當(dāng)0<x≤86時,f(x)遞減,
∴f(x)≥f(86)=學(xué).files/image253.gif) =
=學(xué).files/image255.gif) .
.
∴f(x)min=f(86),此時216-x=130.
當(dāng)87≤x<216時,f(x)遞增,
∴f(x)≥f(87)=學(xué).files/image257.gif) =
=學(xué).files/image255.gif) .
.
∴f(x)min=f(87),此時216-x=129.
∴f(x)min=f(86)=f(87)=學(xué).files/image255.gif) .
.
∴加工G型裝置,H型裝置的人數(shù)分別為86、130或87、129……………………14分
18. (Ⅰ)由題設(shè)知學(xué).files/image260.gif)
由于學(xué).files/image123.gif) ,則有
,則有學(xué).files/image262.gif) ,所以點
,所以點學(xué).files/image119.gif) 的坐標(biāo)為
的坐標(biāo)為學(xué).files/image264.gif) ……..2分
……..2分
故學(xué).files/image127.gif) 所在直線方程為
所在直線方程為學(xué).files/image266.gif) …………3分
…………3分
所以坐標(biāo)原點學(xué).files/image125.gif) 到直線
到直線學(xué).files/image127.gif) 的距離為
的距離為學(xué).files/image268.gif)
又學(xué).files/image270.gif) ,所以
,所以學(xué).files/image272.gif) 解得:
解得:學(xué).files/image274.gif) …………5分
…………5分
所求橢圓的方程為學(xué).files/image276.gif) …………6分
…………6分
(Ⅱ)由題意可知直線學(xué).files/image133.gif) 的斜率存在,設(shè)直線斜率為
的斜率存在,設(shè)直線斜率為學(xué).files/image178.gif)
直線學(xué).files/image133.gif) 的方程為
的方程為學(xué).files/image279.gif) ,則有
,則有學(xué).files/image281.gif) …………8分
…………8分
設(shè)學(xué).files/image283.gif) ,由于
,由于學(xué).files/image131.gif) 、
、學(xué).files/image285.gif) 、
、學(xué).files/image140.gif) 三點共線,且
三點共線,且學(xué).files/image287.gif)
根據(jù)題意得學(xué).files/image289.gif) ,解得
,解得學(xué).files/image291.gif) 或
或學(xué).files/image293.gif) …………14分
…………14分
又學(xué).files/image131.gif) 在橢圓
在橢圓學(xué).files/image121.gif) 上,故
上,故學(xué).files/image295.gif) 或
或學(xué).files/image297.gif)
解得學(xué).files/image299.gif) ,綜上,直線
,綜上,直線學(xué).files/image133.gif) 的斜率為
的斜率為學(xué).files/image301.gif) 或
或學(xué).files/image303.gif) …………16分
…………16分
19. 解:(1)由已知,學(xué).files/image305.gif) (
(學(xué).files/image156.gif) ,
,學(xué).files/image158.gif) ),
),
即學(xué).files/image307.gif) (
(學(xué).files/image156.gif) ,
,學(xué).files/image158.gif) ),且
),且學(xué).files/image309.gif) .
.
∴數(shù)列學(xué).files/image144.gif) 是以
是以學(xué).files/image146.gif) 為首項,公差為1的等差數(shù)列.
為首項,公差為1的等差數(shù)列.
∴學(xué).files/image312.gif) .
.
∴學(xué).files/image317.gif) 恒成立,
恒成立,
∴學(xué).files/image319.gif) 恒成立,
恒成立,
(?)當(dāng)學(xué).files/image150.gif) 為奇數(shù)時,即
為奇數(shù)時,即學(xué).files/image324.gif) 恒成立,
恒成立,
當(dāng)且僅當(dāng)學(xué).files/image326.gif) 時,
時,學(xué).files/image328.gif) 有最小值為1,
有最小值為1,
∴學(xué).files/image330.gif) .
.
當(dāng)且僅當(dāng)學(xué).files/image335.gif) 時,
時,學(xué).files/image337.gif) 有最大值
有最大值學(xué).files/image339.gif) ,
,
∴學(xué).files/image341.gif) .
.
即學(xué).files/image343.gif) ,又
,又學(xué).files/image162.gif) 為非零整數(shù),則
為非零整數(shù),則學(xué).files/image346.gif) .
.
綜上所述,存在學(xué).files/image346.gif) ,使得對任意
,使得對任意學(xué).files/image158.gif) ,都有
,都有學(xué).files/image349.gif) .
.
20.解:(I)學(xué).files/image351.gif) 2分
2分
由學(xué).files/image353.gif) 得,
得,學(xué).files/image355.gif) 或
或學(xué).files/image357.gif)
而學(xué).files/image168.gif) ,列出下表
,列出下表
學(xué).files/image014.gif)
學(xué).files/image359.gif)
0
學(xué).files/image361.gif)
學(xué).files/image363.gif)
學(xué).files/image365.gif)
學(xué).files/image367.gif)
―
0
+
0
―
學(xué).files/image104.gif)
遞減
極小值
遞增
極大值
遞減
所以,當(dāng)學(xué).files/image355.gif) 時,
時,學(xué).files/image104.gif) 取得極小值,極小值等于
取得極小值,極小值等于學(xué).files/image370.gif) ;
;
當(dāng)學(xué).files/image357.gif) 時,
時,學(xué).files/image104.gif) 取得極大值,極大值等于
取得極大值,極大值等于學(xué).files/image372.gif) ;
6分
;
6分
(II)設(shè)函數(shù)學(xué).files/image374.gif) 、
、學(xué).files/image376.gif) , 不妨設(shè)
, 不妨設(shè)學(xué).files/image378.gif)
學(xué).files/image380.gif)
(注:若直接用學(xué).files/image382.gif) 來證明至少扣1分)
10分
來證明至少扣1分)
10分
(III)學(xué).files/image384.gif) 時,
時,
學(xué).files/image386.gif)
學(xué).files/image388.gif)
16分
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com