
題目列表(包括答案和解析)
(本小題滿分10分)選修4—4,坐標(biāo)系與參數(shù)方程
已知曲線 ,直線
,直線 :
: (
( 為參數(shù)).
為參數(shù)).
(I)寫出曲線 的參數(shù)方程,直線
的參數(shù)方程,直線 的普通方程;
的普通方程;
(II)過曲線 上任意一點(diǎn)
上任意一點(diǎn) 作與
作與 夾角為
夾角為 的直線,交
的直線,交 于點(diǎn)
于點(diǎn) ,
, 的最大值與最小值.
的最大值與最小值.
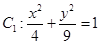 ,直線
,直線 :
: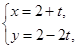 (
(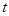 為參數(shù)).
為參數(shù)).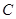 的參數(shù)方程,直線
的參數(shù)方程,直線 的普通方程;
的普通方程;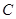 上任意一點(diǎn)
上任意一點(diǎn)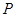 作與
作與 夾角為
夾角為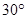 的直線,交
的直線,交 于點(diǎn)
于點(diǎn)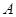 ,
,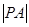 的最大值與最小值.
的最大值與最小值.(本小題滿分10分)
選修4-4:坐標(biāo)系與參數(shù)方程選講
已知曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).
為參數(shù)).
(1)若將曲線![]() 與
與![]() 上各點(diǎn)的橫坐標(biāo)都縮短為原來的一半,分別得到曲線
上各點(diǎn)的橫坐標(biāo)都縮短為原來的一半,分別得到曲線![]() 和
和![]() ,求出曲線
,求出曲線![]() 和
和![]() 的普通方程;
的普通方程;
(2)以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系,求過極點(diǎn)且與
軸的非負(fù)半軸為極軸建立極坐標(biāo)系,求過極點(diǎn)且與![]() 垂直
垂直![]() 的直線的極坐標(biāo)方程.
的直線的極坐標(biāo)方程.
(本小題滿分10分)選修4—4:坐標(biāo)系與參數(shù)方程
在極坐標(biāo)系下,已知圓O:![]() 和直線
和直線![]() ,
,
(1)求圓O和直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)當(dāng)![]() 時(shí),求直線
時(shí),求直線![]() 與圓O公共點(diǎn)的一個(gè)極坐標(biāo).
與圓O公共點(diǎn)的一個(gè)極坐標(biāo).
(本小題滿分10分)
選修4-4:坐標(biāo)系與參數(shù)方程選講
已知曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).
為參數(shù)).
(1)若將曲線![]() 與
與![]() 上各點(diǎn)的橫坐標(biāo)都縮短為原來的一半,分別得到曲線
上各點(diǎn)的橫坐標(biāo)都縮短為原來的一半,分別得到曲線![]() 和
和![]() ,求出曲線
,求出曲線![]() 和
和![]() 的普通方程;
的普通方程;
(2)以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系,求過極點(diǎn)且與
軸的非負(fù)半軸為極軸建立極坐標(biāo)系,求過極點(diǎn)且與![]() 垂直
垂直![]() 的直線的極坐標(biāo)方程.
的直線的極坐標(biāo)方程.
一、選擇題:(每小題5分,共12小題,滿分60分)
題號(hào)
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
A
B
D
C
C
A
C
B
C
A
二、填空題:(每小題5分,共4小題,滿分20分)
13、 14、
14、
15、 16、 ① ③
16、 ① ③
三、解答題答案及評(píng)分標(biāo)準(zhǔn):
17解:(I)
 ,
, ,
,


 =
= ?
?

 …………………………4分
…………………………4分

 =
=  .
.
|