
題目列表(包括答案和解析)
一自來水廠用蓄水池通過管道向所管轄區域供水.某日凌晨,已知蓄水池有水9千噸,水廠計劃在當日每小時向蓄水池注入水2千噸,且每 小時通過管道向所管轄區域供水
小時通過管道向所管轄區域供水 千噸.
千噸.
(1)多少小時后,蓄水池存水量最少?
(2)當蓄水池存水量少于3千噸時,供水就會出現緊張現象,那么當日出現這種情況的時間有多長?
【解析】第一問中(1)設 小時后,蓄水池有水
小時后,蓄水池有水 千噸.依題意,
千噸.依題意, 當
當 ,即
,即 (小時)時,蓄水池的水量最少,只有1千噸
(小時)時,蓄水池的水量最少,只有1千噸
第二問依題意, 解得:
解得:
解:(1)設 小時后,蓄水池有水
小時后,蓄水池有水 千噸.………………………………………1分
千噸.………………………………………1分
依題意, …………………………………………4分
…………………………………………4分
當 ,即
,即 (小時)時,蓄水池的水量最少,只有1千噸. ………2分
(小時)時,蓄水池的水量最少,只有1千噸. ………2分
(2)依題意, ………………………………………………3分
………………………………………………3分
解得: . …………………………………………………………………3分
. …………………………………………………………………3分
所以,當天有8小時會出現供水緊張的情況
在平面直角坐標系 中,曲線
中,曲線 與坐標軸的交點都在圓
與坐標軸的交點都在圓 上.
上.
(1)求圓 的方程;
的方程;
(2)若圓 與直線
與直線 交于
交于 、
、 兩點,且
兩點,且 ,求
,求 的值.
的值.
【解析】本試題主要是考查了直線與圓的位置關系的運用。
(1)曲線 與
與 軸的交點為(0,1),
軸的交點為(0,1),
與 軸的交點為(3+2
軸的交點為(3+2 ,0),(3-2
,0),(3-2 ,0) 故可設
,0) 故可設 的圓心為(3,t),則有32+(t-1)2=(2
的圓心為(3,t),則有32+(t-1)2=(2 )2+t2,解得t=1.
)2+t2,解得t=1.
(2)因為圓 與直線
與直線 交于
交于 、
、 兩點,且
兩點,且 。聯立方程組得到結論。
。聯立方程組得到結論。
已知奇函數![]() 時,取極小值
時,取極小值![]()
![]()
![]()
(1)求![]() 的解析式;
的解析式;
(2)試判斷:當![]() 的圖象上是否存在兩點,使這兩點處的切線的夾角等于45°
的圖象上是否存在兩點,使這兩點處的切線的夾角等于45°
(3)試判斷方程![]() 上是否有解?若有,指出解的個數,若沒有.說明理由.
上是否有解?若有,指出解的個數,若沒有.說明理由.
已知向量 (
( ),向量
),向量 ,
, ,
,
且

 .
.
(Ⅰ)求向量 ;
(Ⅱ)若
;
(Ⅱ)若 ,
, ,求
,求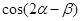 .
.
【解析】本試題主要考查了向量的數量積的運算,以及兩角和差的三角函數關系式的運用。
(1)問中∵ ,∴
,∴ ,…………………1分
,…………………1分
∵ ,得到三角關系是
,得到三角關系是 ,結合
,結合 ,解得。
,解得。
(2)由 ,解得
,解得 ,
, ,結合二倍角公式
,結合二倍角公式 ,和
,和 ,代入到兩角和的三角函數關系式中就可以求解得到。
,代入到兩角和的三角函數關系式中就可以求解得到。
解析一:(Ⅰ)∵ ,∴
,∴ ,…………1分
,…………1分
∵ ,∴
,∴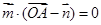 ,即
,即 ① …………2分
① …………2分
又 ② 由①②聯立方程解得,
② 由①②聯立方程解得,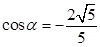 ,
,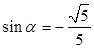 5分
5分
∴ ……………6分
……………6分
(Ⅱ)∵ 即
即 ,
, , …………7分
, …………7分
∴ ,
, ………8分
………8分
又∵ , ………9分
, ………9分
 , ……10分
, ……10分
∴ .
.
解法二: (Ⅰ) ,…………………………………1分
,…………………………………1分
又 ,∴
,∴ ,即
,即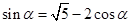 ,①……2分
,①……2分
又 ②
②
將①代入②中,可得 ③ …………………4分
③ …………………4分
將③代入①中,得 ……………………………………5分
……………………………………5分
∴ …………………………………6分
…………………………………6分
(Ⅱ) 方法一
∵ ,
, ,∴
,∴ ,且
,且 ……7分
……7分
∴ ,從而
,從而 . …………………8分
. …………………8分
由(Ⅰ)知 ,
,
 ; ………………9分
; ………………9分
∴ . ………………………………10分
. ………………………………10分
又∵ ,∴
,∴ ,
又
,
又 ,∴
,∴ ……11分
……11分
綜上可得  ………………………………12分
………………………………12分
方法二∵ ,
, ,∴
,∴ ,且
,且 …………7分
…………7分
∴ .
……………8分
.
……………8分
由(Ⅰ)知 ,
, .
…………9分
.
…………9分
∴ ……………10分
……………10分
∵ ,且注意到
,且注意到 ,
,
∴ ,又
,又 ,∴
,∴ ………………………11分
………………………11分
綜上可得  …………………12分
…………………12分
(若用 ,又∵
,又∵ ∴
∴  ,
,
求圓心在直線y=-2x上,并且經過點A(2,-1),與直線x+y=1相切的圓的方程.
【解析】利用圓心和半徑表示圓的方程,首先
設圓心為S,則KSA=1,∴SA的方程為:y+1=x-2,即y=x-3, ………4分
和y=-2x聯立解得x=1,y=-2,即圓心(1,-2)
∴r= =
= ,
,
故所求圓的方程為: +
+ =2
=2
解:法一:
設圓心為S,則KSA=1,∴SA的方程為:y+1=x-2,即y=x-3, ………4分
和y=-2x聯立解得x=1,y=-2,即圓心(1,-2) ……………………8分
∴r= =
= ,
………………………10分
,
………………………10分
故所求圓的方程為: +
+ =2
………………………12分
=2
………………………12分
法二:由條件設所求圓的方程為: +
+ =
=
 , ………………………6分
, ………………………6分
解得a=1,b=-2,  =2
………………………10分
=2
………………………10分
所求圓的方程為: +
+ =2
………………………12分
=2
………………………12分
其它方法相應給分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com