題目列表(包括答案和解析)
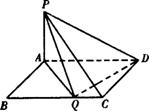
(1)BC邊上是否存在點(diǎn)Q，使得FQ⊥QD，并說(shuō)明理由；
(2)若BC邊上存在唯一的點(diǎn)Q使得FQ⊥QD，指出點(diǎn)Q的位置，并求出此時(shí)AD與平面PDQ所成的角的正弦值；
(3)在(2)的條件下，求二面角Q-PD-A的正弦值．
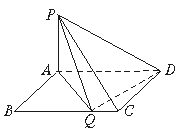
如上圖，矩形ABCD中，|AB|=1，|BC|=a,PA⊥面ABCD且|PA|=1.
(1)BC邊上是否存在點(diǎn)Q，使得PQ⊥QD，并說(shuō)明理由；
(2)若BC邊上存在唯一的點(diǎn)Q使得PQ⊥QD,指出點(diǎn)Q的位置，并求出此時(shí)AD與平面PDQ所成的角的正弦值；
(3)在(2)的條件下，求二面角Q—PD—A的正弦值.
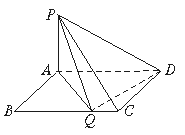
如上圖，矩形ABCD中，|AB|=1，|BC|=a,PA⊥面ABCD且|PA|=1.
(1)BC邊上是否存在點(diǎn)Q，使得PQ⊥QD，并說(shuō)明理由；
(2)若BC邊上存在唯一的點(diǎn)Q使得PQ⊥QD,指出點(diǎn)Q的位置，并求出此時(shí)AD與平面PDQ所成的角的正弦值；
(3)在(2)的條件下，求二面角Q—PD—A的正弦值.
| |||||||||||
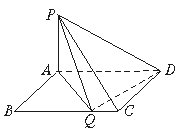
如圖，矩形ABCD中，|AB|=1，|BC|=a，PA⊥面ABCD且|PA|=1．
(1)BC邊上是否存在點(diǎn)Q，使得PQ⊥QD，并說(shuō)明理由；
(2)若BC邊上存在唯一的點(diǎn)Q使得PQ⊥QD，指出點(diǎn)Q的位置，并求出此時(shí)AD與平面PDQ所成的角的正弦值；
(3)在(2)的條件下，求二面角Q—PD—A的正弦值．
一、 A C C D A B D B A C D C
二、13. 
14. ①甲乙的平均數(shù)相同，均為85；② 甲乙的中位數(shù)相同，均為86； ③乙的成績(jī)較穩(wěn)定，甲的成績(jī)波動(dòng)性較大；…… 15.
16.
三、17（Ⅰ）
=
=
由
得，
或
由
得 
或
.
故函數(shù)
的零點(diǎn)為
和
. ……………………………………6分
（Ⅱ）由
，
得 
由
得 
.又
由
得 
，
……………………………………12分
18. 由三視圖可知：
，底面ABCD為直角梯形,，PB=BC=CD=1,AB=2
…………3分
(Ⅱ) 當(dāng)M為PB的中點(diǎn)時(shí)CM∥平面PDA.
取PB中點(diǎn)N,連結(jié)MN，DN，可證MN∥DN且MN＝DN
∴CM∥DN，∴CM∥平面PDA …………6分
(Ⅲ)分別以BC、BA、BP所在直線為x軸、y軸、z軸，建立空間直角坐標(biāo)系.
假設(shè)在BC邊上存在點(diǎn)Q，使得二面角A-PD-Q為
∴
同理，
，可得
=
，
解得
………………………………………12分
19. （Ⅰ）設(shè)“世博會(huì)會(huì)徽”卡有
張，由
,得=6.
故“海寶”卡有4張. 抽獎(jiǎng)?wù)攉@獎(jiǎng)的概率為
.
…………6分
（Ⅱ）
， 
的分布列為 
或
1
2
3
4
p
………………………………12分
20. （Ⅰ）證明 設(shè)
相減得 
注意到 
有
即
…………………………………………5分
（Ⅱ）①設(shè)
由垂徑定理，
即 
化簡(jiǎn)得 
當(dāng)
與
軸平行時(shí)，
的坐標(biāo)也滿足方程.
故所求的中點(diǎn)的軌跡
的方程為；
…………………………………………8分
②
假設(shè)過(guò)點(diǎn)P(1,1)
作直線
與有心圓錐曲線
交于
兩點(diǎn)，且P為
的中點(diǎn)，則
由于
直線
，即
，代入曲線
的方程得
即 
由 
得
.
故當(dāng)時(shí)，存在這樣的直線，其直線方程為；
當(dāng)
時(shí)，這樣的直線不存在. ………………………………12分
21. （Ⅰ）
由
得 
…………………………3分
當(dāng)
時(shí)，
當(dāng)
時(shí)，
故函數(shù)
的單調(diào)增區(qū)間為
，單調(diào)減區(qū)間為
. ………………………5分
（Ⅱ）由（Ⅰ）
由
得 
當(dāng)
時(shí)，當(dāng)
時(shí)，
在
處取得極大值, 
……………………………………7分
（1）
當(dāng)
時(shí)，
函數(shù)在區(qū)間為
遞減 ，
（2）
當(dāng)
時(shí)， 
，
（3）
當(dāng)
時(shí)，
函數(shù)在區(qū)間為遞增 ，
………………………………………12分
22. （Ⅰ）
…………………………………6分
（Ⅱ）解法1：由
，得
猜想時(shí)，一切
時(shí)
恒成立.
①當(dāng)
時(shí)，
成立.
②設(shè)
時(shí)，
，則由
得
=
時(shí)，
由①②知時(shí)，對(duì)一切，有. ………………………………10分
解法2：假設(shè)
記
，可求
故存在，使恒成立.
…………………………………10分
（Ⅲ）證法1：
，由（Ⅱ）知
…………………………………14分
證法2：
猜想
.數(shù)學(xué)歸納法證明
①當(dāng)時(shí)，成立
②假設(shè)當(dāng)
時(shí)，
成立
由①②對(duì)，成立，下同證法1。
…………………………………14分
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com