
題目列表(包括答案和解析)
| PA |
| PB |
| OA |
| OB |
以下四個關于圓錐曲線的命題中:
①雙曲線 與橢圓
與橢圓 有相同的焦點;
有相同的焦點;
②在平面內, 設 、
、 為兩個定點,
為兩個定點, 為動點,且
為動點,且 ,其中常數
,其中常數 為正實數,則動點
為正實數,則動點 的軌跡為橢圓;
的軌跡為橢圓;
③方程 的兩根可分別作為橢圓和雙曲線的離心率;
的兩根可分別作為橢圓和雙曲線的離心率;
④過雙曲線 的右焦點
的右焦點 作直線
作直線 交雙曲線于
交雙曲線于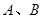 兩點,若
兩點,若 ,則這樣的直線
,則這樣的直線 有且僅有3條。
有且僅有3條。
其中真命題的序號為 (寫出所有真命題的序號).
以下五個關于圓錐曲線的命題中:
①雙曲線 與橢圓
與橢圓 有相同的焦點;
有相同的焦點;
②方程 的兩根可分別作為橢圓和雙曲線的離心率;
的兩根可分別作為橢圓和雙曲線的離心率;
③設A、B為兩個定點, 為常數,若
為常數,若 ,則動點P的軌跡為雙曲線;
,則動點P的軌跡為雙曲線;
④過拋物線 的焦點作直線與拋物線相交于A、B兩點,則使它們的橫坐標之和
的焦點作直線與拋物線相交于A、B兩點,則使它們的橫坐標之和
等于5的直線有且只有兩條。
⑤過定圓C上一點A作圓的動弦AB,O為原點,若 ,則動點P的
,則動點P的
軌跡為橢圓
其中真命題的序號為 (寫出所有真命題的序號)
以下四個關于圓錐曲線的命題中:
①雙曲線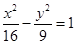 與橢圓
與橢圓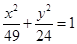 有相同的焦點;
有相同的焦點;
②在平面內, 設 、
、 為兩個定點,
為兩個定點,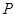 為動點,且
為動點,且 ,其中常數
,其中常數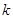 為正實數,則動點
為正實數,則動點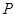 的軌跡為橢圓;
的軌跡為橢圓;
③方程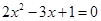 的兩根可分別作為橢圓和雙曲線的離心率;
的兩根可分別作為橢圓和雙曲線的離心率;
④過雙曲線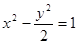 的右焦點
的右焦點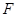 作直線
作直線 交雙曲線于
交雙曲線于 兩點,若
兩點,若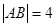 ,則這樣的直線
,則這樣的直線 有且僅有3條。
有且僅有3條。
其中真命題的序號為 (寫出所有真命題的序號).
| PA |
| PB |
| OA |
| OB |
一、 C B C B B AC D A B C D
二、13.  14.
14.  15.
15.  16.3
16.3
三、17(Ⅰ)
= =
=
由 得,
得, 或
或

由 得
得  或
或 .
.
故函數 的零點為
的零點為 和
和 .
……………………………………6分
.
……………………………………6分
(Ⅱ)由
 ,
, 得
得 
由 得
得  .又
.又
由 得
得

 ,
,
 ……………………………………12分
……………………………………12分
18. 由三視圖可知: ,底面ABCD為直角梯形,, BC=CD=1,AB=2
,底面ABCD為直角梯形,, BC=CD=1,AB=2
(Ⅰ)∵  PB⊥DA,梯形ABCD中,PB=BC=CD=1,AB=2 ∴BD=
PB⊥DA,梯形ABCD中,PB=BC=CD=1,AB=2 ∴BD=
又可得DA= ,∴DA⊥BD ,∴DA⊥平面PDB,
,∴DA⊥BD ,∴DA⊥平面PDB,
∴ AD⊥PD ……………………………4分
(Ⅱ) CM∥平面PDA 理由如下:
取PB中點N,連結MN,DN,可證MN∥CD且MN=CD,∴CM∥DN,∴CM∥平面PDA
…………8分
(Ⅲ) 
……………12分
19. (Ⅰ)九年級(1)班應抽取學生10名; ………………………2分
(Ⅱ)通過計算可得九(1)班抽取學生的平均成績為16.5,九(2)班抽取學生的平均成績為17.2.由此可以估計九(1)班學生的平均成績為16.5, 九(2)班學生的平均成績為 17.2 ………………………6分
(Ⅲ)基本事件總數為15,滿足條件的事件數為9 ,故所求事件的概率為
………………………………12分
20. (Ⅰ)證明 設

相減得 
注意到 
有


即
 …………………………………………5分
…………………………………………5分
(Ⅱ)①設
由垂徑定理,
即 
化簡得 
當 與
與 軸平行時,
軸平行時, 的坐標也滿足方程.
的坐標也滿足方程.
故所求 的中點
的中點 的軌跡
的軌跡 的方程為
的方程為 ;
;
…………………………………………8分
②
假設過點P作直線 與有心圓錐曲線
與有心圓錐曲線 交于
交于 兩點,且P為
兩點,且P為 的中點,則
的中點,則

由于

直線 ,即
,即 ,代入曲線
,代入曲線 的方程得
的方程得


故這樣的直線不存在. ……………………………………12分
21.(Ⅰ)函數的定義域為
 由題意易知,
由題意易知,  得
得  ;
;
 當
當 時,
時, 當
當 時,
時,
故函數 的單調增區間為
的單調增區間為 ,單調減區間為
,單調減區間為 . …………………………6分
. …………………………6分
(Ⅱ)
①
當 時,
時,
 在
在 遞減,
遞減, 無極值.
無極值.
②
當 時,由
時,由 得
得 

當 時,
時, 當
當 時,
時,
 時,函數
時,函數 的極大值為
的極大值為
 ;
;
函數 無極小值.
…………………………13分
無極小值.
…………………………13分
22.(Ⅰ)

 …………………………………………4分
…………………………………………4分
(Ⅱ) ,
,
 ……………………………8分
……………………………8分
(Ⅲ)假設

記 ,可求
,可求

故存在 ,使
,使 恒成立.
恒成立.
……………………………………13分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com