91亚洲国产成人久久精品网站,97国产精品,日韩中文字幕无码一区二区三区

變式:設函數.其中【查看更多】

規定C^m_x=

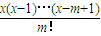，其中x∈R，m是正整數，且C_x=1，這是組合數C^m_n（n、m是正整數，且m≤n）的一種推廣．
（1）求C³_-15的值；
（2）設x＞0，當x為何值時，

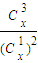取得最小值？
（3）組合數的兩個性質；
①C^m_n=C^n-m_m． ②C^m_n+C^m-1_n=C^m_n+1．
是否都能推廣到C^m_x（x∈R，m是正整數）的情形？若能推廣，則寫出推廣的形式并給出證明；若不能，則說明理由．
變式：規定A_x^m=x（x-1）…（x-m+1），其中x∈R，m為正整數，且A_x=1，這是排列數A_n^m（n，m是正整數，且m≤n）的一種推廣．
（1）求A_-15³的值；
（2）排列數的兩個性質：①A_n^m=nA_n-1^m-1，②A_n^m+mA_n^m-1=A_n+1^m．（其中m，n是正整數）是否都能推廣到A_x^m（x∈R，m是正整數）的情形？若能推廣，寫出推廣的形式并給予證明；若不能，則說明理由；
（3）確定函數A_x³的單調區間．

查看答案和解析>>

已知函數其中為自然對數的底數， .(Ⅰ)設，求函數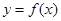的最值；（Ⅱ）若對于任意的，都有成立，求的取值范圍.

【解析】第一問中，當時，，．結合表格和導數的知識判定單調性和極值，進而得到最值。

第二問中，∵，，

∴原不等式等價于：,

即, 亦即

分離參數的思想求解參數的范圍

解：（Ⅰ)當時，，．

當在上變化時，，的變化情況如下表：


－	＋
		1／e

∴時，，．

(Ⅱ)∵，，

∴原不等式等價于：,

即, 亦即．

∴對于任意的，原不等式恒成立,等價于對恒成立,

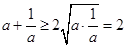∵對于任意的時, （當且僅當時取等號）．

∴只需，即，解之得或.

因此，的取值范圍是

查看答案和解析>>

（本題滿分18分，其中第1小題5分，第2小題5分，第3小題8分）

在平面直角坐標系中，已知為坐標原點，點的坐標為，點的坐標為，其中且.設.

（1）若，，，求方程在區間內的解集；

（2）若點是過點且法向量為的直線上的動點.當時，設函數的值域為集合，不等式的解集為集合. 若恒成立，求實數的最大值；

（3）根據本題條件我們可以知道，函數的性質取決于變量、和的值. 當時，試寫出一個條件，使得函數滿足“圖像關于點對稱，且在處取得最小值”.（說明：請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次，給予不同的評分.）

查看答案和解析>>

（本題滿分18分，其中第1小題5分，第2小題5分，第3小題8分）
在平面直角坐標系中，已知為坐標原點，點的坐標為，點的坐標為，其中且.設.
（1）若，，，求方程在區間內的解集；
（2）若點是過點且法向量為的直線上的動點.當時，設函數的值域為集合，不等式的解集為集合. 若恒成立，求實數的最大值；
（3）根據本題條件我們可以知道，函數的性質取決于變量、和的值. 當時，試寫出一個條件，使得函數滿足“圖像關于點對稱，且在處取得最小值”.（說明：請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次，給予不同的評分.）