
題目列表(包括答案和解析)
給出問題:已知 滿足
滿足 ,試判定
,試判定 的形狀.某學(xué)生的解答如下:
的形狀.某學(xué)生的解答如下:
解:(i)由余弦定理可得,
 ,
,

 ,
,

 ,
,
故 是直角三角形.
是直角三角形.
(ii)設(shè) 外接圓半徑為
外接圓半徑為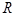 .由正弦定理可得,原式等價于
.由正弦定理可得,原式等價于

 ,
,
故 是等腰三角形.
是等腰三角形.
綜上可知, 是等腰直角三角形.
是等腰直角三角形.
請問:該學(xué)生的解答是否正確?若正確,請在下面橫線中寫出解題過程中主要用到的思想方法;若不正確,請在下面橫線中寫出你認(rèn)為本題正確的結(jié)果. .
已知二次函數(shù)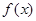 的二次項系數(shù)為
的二次項系數(shù)為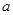 ,且不等式
,且不等式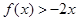 的解集為
的解集為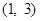 ,
,
(1)若方程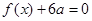 有兩個相等的根,求
有兩個相等的根,求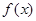 的解析式;
的解析式;
(2)若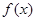 的最大值為正數(shù),求
的最大值為正數(shù),求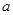 的取值范圍.
的取值范圍.
【解析】第一問中利用∵f(x)+2x>0的解集為(1,3),
設(shè)出二次函數(shù)的解析式,然后利用判別式得到a的值。
第二問中,
解:(1)∵f(x)+2x>0的解集為(1,3),
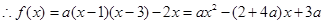 ①
①
由方程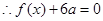
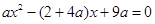 ②
②
∵方程②有兩個相等的根,
∴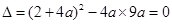 ,
,
即5a2-4a-1=0,解得a=1(舍) 或 a=-1/5
a=-1/5代入①得: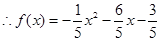
(2)由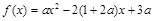
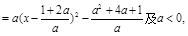
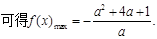
由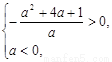 解得:
解得:
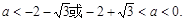
故當(dāng)f(x)的最大值為正數(shù)時,實數(shù)a的取值范圍是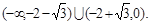
學(xué)校要用三輛車從北湖校區(qū)把教師接到文廟校區(qū),已知從北湖校區(qū)到文廟校區(qū)有兩條公路,汽車走公路①堵車的概率為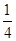 ,不堵車的概率為
,不堵車的概率為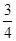 ;汽車走公路②堵車的概率為
;汽車走公路②堵車的概率為 ,不堵車的概率為
,不堵車的概率為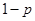 ,若甲、乙兩輛汽車走公路①,丙汽車由于其他原因走公路②,且三輛車是否堵車相互之間沒有影響。(I)若三輛車中恰有一輛車被堵的概率為
,若甲、乙兩輛汽車走公路①,丙汽車由于其他原因走公路②,且三輛車是否堵車相互之間沒有影響。(I)若三輛車中恰有一輛車被堵的概率為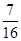 ,求走公路②堵車的概率;(Ⅱ)在(I)的條件下,求三輛車中被堵車輛的個數(shù)
,求走公路②堵車的概率;(Ⅱ)在(I)的條件下,求三輛車中被堵車輛的個數(shù) 的分布列和數(shù)學(xué)期望。
的分布列和數(shù)學(xué)期望。
【解析】第一問中,由已知條件結(jié)合n此獨立重復(fù)試驗的概率公式可知,得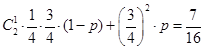
第二問中 可能的取值為0,1,2,3
可能的取值為0,1,2,3 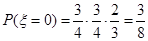 ,
, 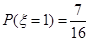
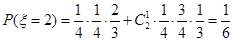 ,
,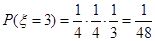
從而得到分布列和期望值
解:(I)由已知條件得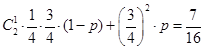 ,即
,即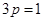 ,則
,則 的值為
的值為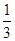 。
。
(Ⅱ) 可能的取值為0,1,2,3
可能的取值為0,1,2,3 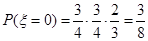 ,
, 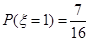
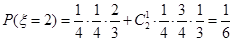 ,
,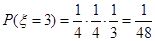
 的分布列為:(1分)
的分布列為:(1分)
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
所以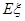
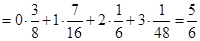
如圖,已知圓錐體 的側(cè)面積為
的側(cè)面積為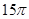 ,底面半徑
,底面半徑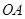 和
和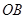 互相垂直,且
互相垂直,且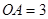 ,
, 是母線
是母線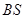 的中點.
的中點.

(1)求圓錐體的體積;
(2)異面直線 與
與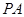 所成角的大小(結(jié)果用反三角函數(shù)表示).
所成角的大小(結(jié)果用反三角函數(shù)表示).
【解析】本試題主要考查了圓錐的體積和異面直線的所成的角的大小的求解。
第一問中,由題意, 得
得 ,故
,故
從而體積 .2中取OB中點H,聯(lián)結(jié)PH,AH.
.2中取OB中點H,聯(lián)結(jié)PH,AH.
由P是SB的中點知PH//SO,則 (或其補角)就是異面直線SO與PA所成角.
(或其補角)就是異面直線SO與PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.在
AH.在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
則 ,所以異面直線SO與P成角的大arctan
,所以異面直線SO與P成角的大arctan
解:(1)由題意, 得
得 ,
,
故 從而體積
從而體積 .
.
(2)如圖2,取OB中點H,聯(lián)結(jié)PH,AH.
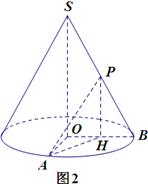
由P是SB的中點知PH//SO,則 (或其補角)就是異面直線SO與PA所成角.
(或其補角)就是異面直線SO與PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.
AH.
在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
則 ,所以異面直線SO與P成角的大arctan
,所以異面直線SO與P成角的大arctan
如圖,測量河對岸的塔高 時,可以選與塔底
時,可以選與塔底 在同一水平面內(nèi)的兩個測點
在同一水平面內(nèi)的兩個測點 .現(xiàn)測得
.現(xiàn)測得
 ,并在點
,并在點 測得塔頂
測得塔頂 的仰角為
的仰角為 ,
求塔高
,
求塔高 (精確到
(精確到 ,
, )
)

【解析】本試題主要考查了解三角形的運用,利用正弦定理在 中,得到
中,得到 ,然后在
,然后在 中,利用正切值可知
中,利用正切值可知
解:在 中,
中,
由正弦定理得: ,所以
,所以 
在 中,
中,
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com