
題目列表(包括答案和解析)
已知點(diǎn)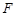 為拋物線
為拋物線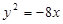 的焦點(diǎn),
的焦點(diǎn),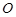 為原點(diǎn),點(diǎn)
為原點(diǎn),點(diǎn)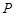 是拋物線準(zhǔn)線上一動(dòng)點(diǎn),點(diǎn)
是拋物線準(zhǔn)線上一動(dòng)點(diǎn),點(diǎn)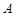 在拋物線上,且
在拋物線上,且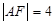 ,則
,則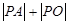 的最小值為 ( )
的最小值為 ( )
A.6
B.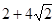 C.
C.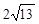 D.
D.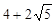
已知點(diǎn)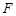 為拋物線
為拋物線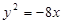 的焦點(diǎn),
的焦點(diǎn),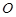 為原點(diǎn),點(diǎn)
為原點(diǎn),點(diǎn)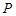 是拋物線準(zhǔn)線上一動(dòng)點(diǎn),點(diǎn)
是拋物線準(zhǔn)線上一動(dòng)點(diǎn),點(diǎn)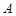 在拋物線上,且
在拋物線上,且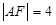 ,則
,則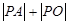 的最小值為 ( )
的最小值為 ( )
A.6 B. C.
C.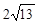 D.
D.
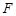 為拋物線
為拋物線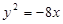 的焦點(diǎn),
的焦點(diǎn),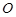 為原點(diǎn),點(diǎn)
為原點(diǎn),點(diǎn)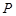 是拋物線準(zhǔn)線上一動(dòng)點(diǎn),點(diǎn)
是拋物線準(zhǔn)線上一動(dòng)點(diǎn),點(diǎn)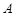 在拋物線上,且
在拋物線上,且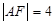 ,則
,則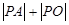 的最小值為 ( )
的最小值為 ( )| A.6 | B. | C. | D. |
已知點(diǎn) 為拋物線
為拋物線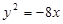 的焦點(diǎn),
的焦點(diǎn), 為原點(diǎn),點(diǎn)
為原點(diǎn),點(diǎn) 是拋物線準(zhǔn)線上一動(dòng)點(diǎn),點(diǎn)
是拋物線準(zhǔn)線上一動(dòng)點(diǎn),點(diǎn) 在拋物線上,且
在拋物線上,且 ,則
,則 的最小值為 ( )
的最小值為 ( )
| A.6 | B. | C.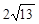 | D. |
(09年朝陽區(qū)統(tǒng)考)(14分)
已知點(diǎn)![]() 為拋物線
為拋物線![]() 的焦點(diǎn),點(diǎn)
的焦點(diǎn),點(diǎn)![]() 是準(zhǔn)線
是準(zhǔn)線![]() 上的動(dòng)點(diǎn),直線
上的動(dòng)點(diǎn),直線![]() 交拋物線
交拋物線![]() 于
于![]() 兩點(diǎn),若點(diǎn)
兩點(diǎn),若點(diǎn)![]() 的縱坐標(biāo)為
的縱坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 為準(zhǔn)線
為準(zhǔn)線![]() 與
與![]() 軸的交點(diǎn).
軸的交點(diǎn).
(Ⅰ)求直線![]() 的方程;
的方程;
(Ⅱ)求![]() 的面積
的面積![]() 范圍;
范圍;
(Ⅲ)設(shè)![]() ,
,![]() ,求證
,求證![]() 為定值.
為定值.

一、選擇題
C B B A B A A A DD C C
二、填空題
13. 學(xué)文科.files/image235.gif) 14. ―4 15.
2880 16.①③
14. ―4 15.
2880 16.①③
17.解,由題意知,在甲盒中放一球概率為學(xué)文科.files/image237.gif) ,在乙盒放一球的概率為
,在乙盒放一球的概率為學(xué)文科.files/image030.gif) ….3分
….3分
①當(dāng)n=3時(shí),學(xué)文科.files/image240.gif) 的概率為
的概率為學(xué)文科.files/image242.gif) …6分
…6分
②學(xué)文科.files/image141.gif) 時(shí),有
時(shí),有學(xué)文科.files/image245.gif) 或
或學(xué)文科.files/image247.gif)
它的概率為學(xué)文科.files/image249.gif) ….12分
….12分
18.解: (1)解:在學(xué)文科.files/image076.gif) 中
中 學(xué)文科.files/image252.gif)
學(xué)文科.files/image254.gif)
學(xué)文科.files/image256.gif) 2分
2分
學(xué)文科.files/image258.gif)
學(xué)文科.files/image256.gif) 4分
4分
學(xué)文科.files/image260.gif)
學(xué)文科.files/image262.gif)
學(xué)文科.files/image264.gif)
學(xué)文科.files/image266.gif)
學(xué)文科.files/image256.gif) 6分
6分
(2)學(xué)文科.files/image148.gif) =
=學(xué)文科.files/image268.gif)
學(xué)文科.files/image256.gif) 12分
12分
19. (法一)(1)證明:取學(xué)文科.files/image270.gif) 中點(diǎn)
中點(diǎn)學(xué)文科.files/image272.gif) ,連接
,連接學(xué)文科.files/image274.gif) 、
、學(xué)文科.files/image276.gif) .
.
∵△學(xué)文科.files/image278.gif) 是等邊三角形,∴
是等邊三角形,∴學(xué)文科.files/image274.gif) ⊥
⊥學(xué)文科.files/image270.gif) ,
,
又平面學(xué)文科.files/image278.gif) ⊥平面
⊥平面學(xué)文科.files/image156.gif) ,
,
∴學(xué)文科.files/image274.gif) ⊥平面
⊥平面學(xué)文科.files/image156.gif) ,∴
,∴學(xué)文科.files/image166.gif) 在平面
在平面學(xué)文科.files/image156.gif) 內(nèi)射影是
內(nèi)射影是學(xué)文科.files/image283.gif) ,
,
∵學(xué)文科.files/image285.gif) =2,
=2,學(xué)文科.files/image287.gif) ,
,學(xué)文科.files/image289.gif) ,
,學(xué)文科.files/image291.gif) ,
,
∴△學(xué)文科.files/image293.gif) ∽△
∽△學(xué)文科.files/image295.gif) ,∴
,∴學(xué)文科.files/image297.gif) .
.
又學(xué)文科.files/image299.gif) °,∴
°,∴學(xué)文科.files/image301.gif) °,
°,
∴學(xué)文科.files/image303.gif) °,∴
°,∴學(xué)文科.files/image164.gif) ⊥
⊥學(xué)文科.files/image276.gif) ,
,
由三垂線定理知學(xué)文科.files/image164.gif) ⊥
⊥學(xué)文科.files/image166.gif) ……….(6分)
……….(6分)
(2)取AP的中點(diǎn)E及PD的中點(diǎn)F,連ME、CF則CFEM為平行四邊形,CF學(xué)文科.files/image308.gif) 平面PAD所以ME
平面PAD所以ME學(xué)文科.files/image308.gif) 平面PAD,所以平面MPA
平面PAD,所以平面MPA學(xué)文科.files/image308.gif) 平面PAD所以二面角M―PA―D為900.(12分)
平面PAD所以二面角M―PA―D為900.(12分)
20.解:(1)學(xué)文科.files/image310.gif)
學(xué)文科.files/image312.gif)
學(xué)文科.files/image256.gif) 2分
2分
學(xué)文科.files/image139.gif)
學(xué)文科.files/image315.gif)
-1
學(xué)文科.files/image317.gif)
學(xué)文科.files/image319.gif)
學(xué)文科.files/image321.gif)
學(xué)文科.files/image323.gif) (x)
(x)
-
0
+
0
-
學(xué)文科.files/image325.gif) (x)
(x)
減
極小值0
增
極大值學(xué)文科.files/image327.gif)
減
學(xué)文科.files/image329.gif)
學(xué)文科.files/image256.gif) 6分
6分
(2)學(xué)文科.files/image331.gif)
學(xué)文科.files/image333.gif)
學(xué)文科.files/image335.gif)
學(xué)文科.files/image337.gif)
學(xué)文科.files/image339.gif)
學(xué)文科.files/image256.gif) 8分
8分
學(xué)文科.files/image341.gif)
學(xué)文科.files/image256.gif) 12分
12分
21.Ⅰ)由題知點(diǎn)學(xué)文科.files/image343.gif) 的坐標(biāo)分別為
的坐標(biāo)分別為學(xué)文科.files/image345.gif) ,
,學(xué)文科.files/image347.gif) ,
,
于是直線學(xué)文科.files/image201.gif) 的斜率為
的斜率為學(xué)文科.files/image349.gif) ,
,
所以直線學(xué)文科.files/image201.gif) 的方程為
的方程為學(xué)文科.files/image351.gif) ,即為
,即為學(xué)文科.files/image353.gif) .…………………4分
.…………………4分
(Ⅱ)設(shè)學(xué)文科.files/image205.gif) 兩點(diǎn)的坐標(biāo)分別為
兩點(diǎn)的坐標(biāo)分別為學(xué)文科.files/image356.gif) ,
,
由學(xué)文科.files/image358.gif) 得
得學(xué)文科.files/image360.gif) ,
,
所以學(xué)文科.files/image362.gif) ,
,學(xué)文科.files/image364.gif) .
.
于是學(xué)文科.files/image366.gif) .
.
點(diǎn)學(xué)文科.files/image210.gif) 到直線
到直線學(xué)文科.files/image353.gif) 的距離
的距離學(xué)文科.files/image369.gif) ,
,
所以學(xué)文科.files/image371.gif) .
.
因?yàn)?sub>學(xué)文科.files/image373.gif)
學(xué)文科.files/image375.gif) 且
且學(xué)文科.files/image377.gif) ,于是
,于是學(xué)文科.files/image379.gif) ,
,
所以學(xué)文科.files/image213.gif) 的面積
的面積學(xué)文科.files/image215.gif) 范圍是
范圍是學(xué)文科.files/image381.gif) .
…………………………………8分
.
…………………………………8分
(Ⅲ)由(Ⅱ)及學(xué)文科.files/image217.gif) ,
,學(xué)文科.files/image219.gif) ,得
,得
學(xué)文科.files/image384.gif) ,
,學(xué)文科.files/image386.gif) ,
,
于是學(xué)文科.files/image388.gif) ,
,學(xué)文科.files/image390.gif) (
(學(xué)文科.files/image392.gif) ).
).
所以學(xué)文科.files/image394.gif) .
.
所以學(xué)文科.files/image221.gif) 為定值
為定值學(xué)文科.files/image396.gif) .
……………………………………………12分
.
……………………………………………12分
22.解(Ⅰ)由學(xué)文科.files/image398.gif) 得,
得,學(xué)文科.files/image400.gif)
學(xué)文科.files/image402.gif)
學(xué)文科.files/image404.gif)
數(shù)列{an}的通項(xiàng)公式為學(xué)文科.files/image406.gif) 4分
4分
(Ⅱ)學(xué)文科.files/image408.gif)
設(shè)學(xué)文科.files/image410.gif) ①
①
學(xué)文科.files/image412.gif) ②
②
①―②得
學(xué)文科.files/image414.gif)
=學(xué)文科.files/image416.gif)
學(xué)文科.files/image418.gif)
即數(shù)列學(xué)文科.files/image420.gif) 的前n項(xiàng)和為
的前n項(xiàng)和為學(xué)文科.files/image422.gif) 9分
9分
(Ⅲ)解法1:學(xué)文科.files/image424.gif) 不等式
不等式學(xué)文科.files/image231.gif) 恒成立,
恒成立,
即學(xué)文科.files/image427.gif) 對(duì)于一切的
對(duì)于一切的學(xué)文科.files/image233.gif) 恒成立
恒成立
設(shè)學(xué)文科.files/image429.gif) ,當(dāng)k>4時(shí),由于對(duì)稱軸
,當(dāng)k>4時(shí),由于對(duì)稱軸學(xué)文科.files/image431.gif) ,且
,且學(xué)文科.files/image433.gif) 而函數(shù)
而函數(shù)學(xué)文科.files/image435.gif) 在
在學(xué)文科.files/image437.gif) 是增函數(shù),
是增函數(shù),學(xué)文科.files/image439.gif) 不等式
不等式學(xué)文科.files/image231.gif) 恒成立
恒成立
即當(dāng)k<4時(shí),不等式學(xué)文科.files/image231.gif) 對(duì)于一切的
對(duì)于一切的學(xué)文科.files/image233.gif) 恒成立 14分
恒成立 14分
解法2:bn=n(2n-1),不等式學(xué)文科.files/image231.gif) 恒成立,即
恒成立,即學(xué)文科.files/image427.gif) 對(duì)于一切
對(duì)于一切學(xué)文科.files/image233.gif) 恒成立
恒成立
學(xué)文科.files/image443.gif) 而k>4
而k>4
學(xué)文科.files/image445.gif) 恒成立,故當(dāng)k>4時(shí),不等式
恒成立,故當(dāng)k>4時(shí),不等式學(xué)文科.files/image231.gif) 對(duì)于一切的
對(duì)于一切的學(xué)文科.files/image233.gif) 恒成立 (14分)
恒成立 (14分)
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com