20080416
二、填空題:每題5分,共20分)
13.學(xué)理科.files/image098.gif) 14.
14.學(xué)理科.files/image100.gif) 或
或學(xué)理科.files/image102.gif) 或
或學(xué)理科.files/image104.gif) ; 15.a=-1或a=-
; 15.a=-1或a=-學(xué)理科.files/image038.gif) ;
;
16.①④
17.解:(1)學(xué)理科.files/image106.gif) ,
,
學(xué)理科.files/image108.gif) .又
.又學(xué)理科.files/image110.gif) ,
,學(xué)理科.files/image112.gif) .(6分)
.(6分)
(2)由學(xué)理科.files/image114.gif) 且
且學(xué)理科.files/image116.gif) ,
,
得學(xué)理科.files/image118.gif) .
.學(xué)理科.files/image120.gif) ,
,學(xué)理科.files/image122.gif) .(6分)
.(6分)
18.證法一:向量法
證法二:(1)由已知有BC⊥AB,BC⊥B1B,∴BC⊥平面ABB1A1
又A1E在平面ABB1A1內(nèi) ∴有BC⊥A1E
(2)取B1C的中點(diǎn)D,連接FD、BD
學(xué)理科.files/image123.gif) ∵F、D分別是AC1、B1C之中點(diǎn),∴FD∥
∵F、D分別是AC1、B1C之中點(diǎn),∴FD∥學(xué)理科.files/image018.gif) A1B1∥BE
A1B1∥BE
∴四邊形EFBD為平行四邊形
∴EF∥BD
又BD學(xué)理科.files/image125.gif) 平面BCC1B1
平面BCC1B1
∴EF∥面BCC1B1
(3)過B1作B1H⊥CEFH,連BH,又B1B⊥面BAC,B1H⊥CE
∴BH⊥EC ∴∠B1HB為二面角B1-EC-B平面角
在Rt△BCE中有BE=學(xué)理科.files/image127.gif) ,BC=
,BC=學(xué)理科.files/image079.gif) ,CE=
,CE=學(xué)理科.files/image129.gif) ,BH=
,BH=學(xué)理科.files/image131.gif)
又∠A1CA=學(xué)理科.files/image077.gif) ∴BB1=AA1=AC=2
∴BB1=AA1=AC=2
∴tan∠B1HB=學(xué)理科.files/image134.gif)
19.解(1)由已知圓的標(biāo)準(zhǔn)方程為:(x-aCosφ)2+(y-aSinφ)2=a2(a>0)
設(shè)圓的圓心坐標(biāo)為(x,y),
則學(xué)理科.files/image136.gif) (
(學(xué)理科.files/image083.gif) 為參數(shù)),消參數(shù)得圓心的軌跡方程為:x2+y2=a2,(5分)
為參數(shù)),消參數(shù)得圓心的軌跡方程為:x2+y2=a2,(5分)
(2)有方程組學(xué)理科.files/image139.gif) 得公共弦的方
得公共弦的方
程:學(xué)理科.files/image141.gif) 圓X2+Y2=a2的圓心到公共弦的距離d=
圓X2+Y2=a2的圓心到公共弦的距離d=學(xué)理科.files/image143.gif) ,(定值)
,(定值)
∴弦長l=學(xué)理科.files/image145.gif) (定值) (5分)
(定值) (5分)
20.(1)合格結(jié)果:0,1,2,3 相應(yīng)月盈利額X=-30,5,40,75
(2)P(X≥40)=P(X=40)+P(X=75)=學(xué)理科.files/image147.gif)
(3)
X
-30
5
40
75
P
學(xué)理科.files/image149.gif)
學(xué)理科.files/image151.gif)
學(xué)理科.files/image153.gif)
學(xué)理科.files/image155.gif)
EX=54(元) ∴6個月平均:6×54=324(元)
21.(1)由已知:學(xué)理科.files/image157.gif)
依題意得:學(xué)理科.files/image159.gif) ≥0對x∈
≥0對x∈學(xué)理科.files/image090.gif) 成立
成立
∴ax-1≥0,對x∈學(xué)理科.files/image090.gif) 恒成立,即a≥
恒成立,即a≥學(xué)理科.files/image163.gif) ,對x∈
,對x∈學(xué)理科.files/image090.gif) 恒成立,
恒成立,
∴a≥(學(xué)理科.files/image163.gif) )max,即a≥1.
)max,即a≥1.
(2)當(dāng)a=1時,學(xué)理科.files/image166.gif) ,x∈[
,x∈[學(xué)理科.files/image018.gif) ,2],若x∈
,2],若x∈學(xué)理科.files/image168.gif) ,則
,則學(xué)理科.files/image170.gif) ,
,
若x∈學(xué)理科.files/image172.gif) ,則
,則學(xué)理科.files/image174.gif) ,故x=1是函數(shù)f(x)在區(qū)間[
,故x=1是函數(shù)f(x)在區(qū)間[學(xué)理科.files/image018.gif) ,2]上唯一的極小值點(diǎn),也就是最小值點(diǎn),故f(x)min=f(1)=0.
,2]上唯一的極小值點(diǎn),也就是最小值點(diǎn),故f(x)min=f(1)=0.
又f(學(xué)理科.files/image018.gif) )=1-ln2,f(2)=-
)=1-ln2,f(2)=- 學(xué)理科.files/image018.gif) +ln2,f(
+ln2,f(學(xué)理科.files/image018.gif) )-f(2)=
)-f(2)=學(xué)理科.files/image020.gif) -2ln2=
-2ln2=學(xué)理科.files/image176.gif) ,
,
∵e3>2.73=19.683>16,
∴f(學(xué)理科.files/image018.gif) )-f(2)>0
)-f(2)>0
∴f(學(xué)理科.files/image018.gif) )>f(2)
)>f(2)
∴f(x)在[學(xué)理科.files/image018.gif) ,2]上最大值是f(
,2]上最大值是f(學(xué)理科.files/image018.gif) )
)
∴f(x)在[學(xué)理科.files/image018.gif) ,2]最大1-ln2,最小0
,2]最大1-ln2,最小0
(3)當(dāng)a=1時,由(1)知,f(x)=學(xué)理科.files/image178.gif) +lnx在
+lnx在學(xué)理科.files/image090.gif)
當(dāng)n>1時,令x=學(xué)理科.files/image181.gif) ,則x>1 ∴f(x)>f(1)=0
,則x>1 ∴f(x)>f(1)=0
即學(xué)理科.files/image183.gif)
即ln學(xué)理科.files/image181.gif) >
>學(xué)理科.files/image186.gif)
22.解:(1)設(shè)橢圓方程為學(xué)理科.files/image188.gif) (a>b>0)
(a>b>0)
則學(xué)理科.files/image190.gif) ∴橢圓方程
∴橢圓方程學(xué)理科.files/image192.gif)
(2) ∵直線學(xué)理科.files/image094.gif) ∥DM且在y軸上的截距為m,∴y=
∥DM且在y軸上的截距為m,∴y=學(xué)理科.files/image018.gif) x+m
x+m
由學(xué)理科.files/image195.gif)
∵學(xué)理科.files/image094.gif) 與橢圓交于A、B兩點(diǎn)
與橢圓交于A、B兩點(diǎn)
∴△=(2m)2-4(2m2-4)>0學(xué)理科.files/image197.gif) -2<m<2(m≠0)
-2<m<2(m≠0)
(3)設(shè)直線MA、MB斜率分別為k1,k2,則只要證:k1+k2=0
設(shè)A(x1,y1),B(x2,y2),則k1=學(xué)理科.files/image199.gif) ,k2=
,k2=學(xué)理科.files/image201.gif)
由x2+2mx+2m2-4=0得x1+x2=-2m,x1x2=2m2-4
而k1+k2=學(xué)理科.files/image199.gif) +
+學(xué)理科.files/image201.gif) =
=學(xué)理科.files/image205.gif) (*)
(*)
又y1=學(xué)理科.files/image018.gif) x1+m y2=
x1+m y2=學(xué)理科.files/image018.gif) x2+m
x2+m
∴(*)分子=(學(xué)理科.files/image018.gif) x1+m-1)(x2-2)+(
x1+m-1)(x2-2)+( 學(xué)理科.files/image018.gif) x2+m -1)(x1-2)
x2+m -1)(x1-2)
=x1x2+(m-2)(x1+x2)-4(m-1)
=2m2-4+(m-2)(-m)-4(m-1)
=0
∴k1+k2=0,證之.

![]() -2aySin
-2aySin![]() =0(a>0)
=0(a>0)![]() -2aySin
-2aySin![]() =0(a>0)
=0(a>0)![]() -2aySin
-2aySin![]() =0(a>0)
=0(a>0)![]() -2aySin
-2aySin![]() =0(a>0)
=0(a>0)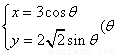 為參數(shù))和定點(diǎn)
為參數(shù))和定點(diǎn)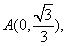 F1,F(xiàn)2是圓錐曲線的左右焦點(diǎn)。
F1,F(xiàn)2是圓錐曲線的左右焦點(diǎn)。