
題目列表(包括答案和解析)
由函數y=f(x)確定數列{an},an=f(n),函數y=f(x)的反函數y="f" -1(x)能確定數列{bn},bn=" f" –1(n),若對于任意nÎN*,都有bn=an,則稱數列{bn}是數列{an}的“自反數列”.
(1)若函數f(x)= 確定數列{an}的自反數列為{bn},求an;
確定數列{an}的自反數列為{bn},求an;
(2)已知正數數列{cn}的前n項之和Sn= (cn+
(cn+ ).寫出Sn表達式,并證明你的結論;
).寫出Sn表達式,并證明你的結論;
(3)在(1)和(2)的條件下,d1=2,當n≥2時,設dn= ,Dn是數列{dn}的前n項之和,且Dn>log a (1-2a)恒成立,求a的取值范圍.
,Dn是數列{dn}的前n項之和,且Dn>log a (1-2a)恒成立,求a的取值范圍.
由函數y=f(x)確定數列{an},an=f(n),函數y=f(x)的反函數y=f -1(x)能確定數列{bn},bn= f –1(n),若對于任意nÎN*,都有bn=an,則稱數列{bn}是數列{an}的“自反數列”.
(1)若函數f(x)= 確定數列{an}的自反數列為{bn},求an;
確定數列{an}的自反數列為{bn},求an;
(2)已知正數數列{cn}的前n項之和Sn= (cn+
(cn+ ).寫出Sn表達式,并證明你的結論;
).寫出Sn表達式,并證明你的結論;
(3)在(1)和(2)的條件下,d1=2,當n≥2時,設dn= ,Dn是數列{dn}的前n項之和,且Dn>log a (1-2a)恒成立,求a的取值范圍.
,Dn是數列{dn}的前n項之和,且Dn>log a (1-2a)恒成立,求a的取值范圍.
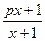 確定數列{an}的自反數列為{bn},求an;
確定數列{an}的自反數列為{bn},求an;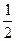 (cn+
(cn+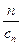 ).寫出Sn表達式,并證明你的結論;
).寫出Sn表達式,并證明你的結論;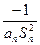 ,Dn是數列{dn}的前n項之和,且Dn>log a (1-2a)恒成立,求a的取值范圍.
,Dn是數列{dn}的前n項之和,且Dn>log a (1-2a)恒成立,求a的取值范圍.由函數y=f(x)確定數列{an},an=f(n),函數y=f(x)的反函數y=f -1(x)能確定數列{bn},bn= f –1(n),若對于任意nÎN*,都有bn=an,則稱數列{bn}是數列{an}的“自反數列”.
(1)若函數f(x)=![]() 確定數列{an}的自反數列為{bn},求an;
確定數列{an}的自反數列為{bn},求an;
(2)已知正數數列{cn}的前n項之和Sn=![]() (cn+
(cn+![]() ).寫出Sn表達式,并證明你的結論;
).寫出Sn表達式,并證明你的結論;
(3)在(1)和(2)的條件下,d1=2,當n≥2時,設dn=![]() ,Dn是數列{dn}的前n項之和,且Dn>log a (1-2a)恒成立,求a的取值范圍.
,Dn是數列{dn}的前n項之和,且Dn>log a (1-2a)恒成立,求a的取值范圍.
參考答案
(本題滿分18分)本題共有3個小題,第1小題滿分3分,第2小題滿分7分,第3小題滿分8分)
由函數y=f(x)確定數列{an},an=f(n),函數y=f(x)的反函數y=f -1(x)能確定數列{bn},bn= f –1(n),若對于任意nÎN*,都有bn=an,則稱數列{bn}是數列{an}的“自反數列”.
(1)若函數f(x)=確定數列{an}的自反數列為{bn},求an;
(2)已知正數數列{cn}的前n項之和Sn=(cn+).寫出Sn表達式,并證明你的結論;
(3)在(1)和(2)的條件下,d1=2,當n≥2時,設dn=,Dn是數列{dn}的前n項之和,且Dn>log a (1-2a)恒成立,求a的取值范圍.
一、選擇題
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
B
D
D
C
D
C
C
D
B
C
|