
題目列表(包括答案和解析)
(本小題為必做題,滿分12分)
甲、乙、丙三個同學一起參加某高校組織的自主招生考試,考試分筆試和面試兩部分,筆試和面試均合格者將成為該高校的預錄取生(可在高考中加分錄取),兩次考試過程相互獨立.根據甲、乙、丙三個同學的平時成績分析,甲、乙、丙三個同學能通過筆試的概率分別是0.6,0.5,0.4,能通過面試的概率分別是0.5,0.6,0.75.
(1)求甲、乙、丙三個同學中恰有一人通過筆試的概率;
(2)設經過兩次考試后,能被該高校預錄取的人數為![]() ,求隨機變量
,求隨機變量![]() 的期望
的期望![]() .
.
(本小題為必做題,滿分12分)
已知直線![]() 被拋物線
被拋物線![]() 截得的弦長
截得的弦長![]() 為20,
為20,![]() 為坐標原點.
為坐標原點.
(1)求實數![]() 的值;
的值;
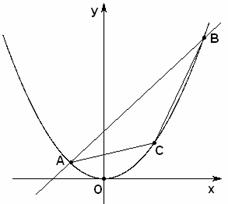 (2)問點
(2)問點![]() 位于拋物線弧
位于拋物線弧![]() 上何處時,△
上何處時,△![]() 面積最大?
面積最大?
(本小題滿分12分)
在一次數學考試中,第21題和第22題為選做題. 規定每位考生必須且只須在其中選做一題. 設4名考生選做每一道題的概率均為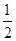 .
.
(1)求其中甲、乙兩名學生選做同一道題的概率;
(2)設這4名考生中選做第22題的學生個數為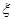 ,求
,求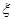 的概率分布及數學期望. 的解析
的概率分布及數學期望. 的解析
(本小題滿分12分)
在一次數學考試中,第21題和第22題為選做題. 規定每位考生必須且只須在其中選做一題. 設4名考生選做這兩題的可能性均為 .
.
(1)求其中甲、乙二名學生選做同一道題的概率;
(2)設這4名考生中選做第22題的學生個數為 ,求
,求 的概率分布及數學期望.
的概率分布及數學期望.
(本小題滿分12分)
在一次數學考試中,第21題和第22題為選做題. 規定每位考生必須且只須在其中選做一題. 設4名考生選做每一道題的概率均為 .
.
(1)求其中甲、乙兩名學生選做同一道題的概率;
(2)設這4名考生中選做第22題的學生個數為 ,求
,求 的概率分布及數學期望. 的解析
的概率分布及數學期望. 的解析
A.必做題部分
一、填空題:(本大題共14小題,每小題5分,共70分.)
1. 2.
2. 3.共線 4.20 5.
3.共線 4.20 5. 6.
6. 7.
7. 8.2,5,10 9.16.4 10.1 11.7 12.
8.2,5,10 9.16.4 10.1 11.7 12. 13.2 14.
13.2 14.
二、解答題:
15.解:(1)

(2)
余弦定理 可得
可得
又∵
∴
16.證明 (1)∵PA⊥底面ABCD,∴AD是PD在平面ABCD內的射影,
(1)∵PA⊥底面ABCD,∴AD是PD在平面ABCD內的射影,
∵CD 平面ABCD且CD⊥AD,∴CD⊥PD
平面ABCD且CD⊥AD,∴CD⊥PD
(2)取CD中點G,連EG、FG,
∵E、F分別是AB、PC的中點,∴EG∥AD,FG∥PD
∴平面EFG∥平面PAD,故EF∥平面PAD
(3)解 當平面PCD與平面ABCD成45°角時,直線EF⊥面PCD
當平面PCD與平面ABCD成45°角時,直線EF⊥面PCD
證明 G為CD中點,則EG⊥CD,由(1)知FG⊥CD,故∠EGF為平面PCD與平面ABCD所成二面角的平面角
G為CD中點,則EG⊥CD,由(1)知FG⊥CD,故∠EGF為平面PCD與平面ABCD所成二面角的平面角 即∠EGF=45°,從而得∠ADP=45°,AD=AP
即∠EGF=45°,從而得∠ADP=45°,AD=AP
由Rt△PAE≌Rt△CBE,得PE=CE
又F是PC的中點,∴EF⊥PC,由CD⊥EG,CD⊥FG,得CD⊥平面EFG,CD⊥EF即EF⊥CD,故EF⊥平面PCD
17.解:(1)依題意, 到
到 距離等于
距離等于 到直線
到直線 的距離,曲線
的距離,曲線 是以原點為頂點,
是以原點為頂點, 為焦點的拋物線
為焦點的拋物線
 曲線
曲線 方程是
方程是
(2)設圓心 ,因為圓
,因為圓 過
過
故設圓的方程
令 得:
得:
設圓與 軸的兩交點為
軸的兩交點為 ,則
,則

 在拋物線
在拋物線 上,
上,


所以,當 運動時,弦長
運動時,弦長 為定值2
為定值2
18.解(1)設日銷售量為
則日利潤
(2)
 ①當2≤a≤4時,33≤a+31≤35,當35 <x<41時,
①當2≤a≤4時,33≤a+31≤35,當35 <x<41時,
∴當x=35時,L(x)取最大值為
②當4<a≤5時,35≤a+31≤36,
易知當x=a+31時,L(x)取最大值為 綜合上得
綜合上得
19.解(1)據題意: 
可行域如圖(暫缺)
 的幾何意義是定點
的幾何意義是定點 到區域內的點
到區域內的點 連線的斜率
連線的斜率 ,
,
又
故 的取值范圍為
的取值范圍為
(2)當 有零點時,
有零點時, ,滿足條件為
,滿足條件為
由拋物線的下方與 圍成的區域面積
圍成的區域面積

由直線 圍成的區域面積
圍成的區域面積
故 有零點的概率
有零點的概率

 無零點的概率為
無零點的概率為
(3) 是
是 函數.
函數.
證明:  符合條件.
符合條件.
因為 ,
,
同理: ;
; 


 .
.
所以,  符合條件.
符合條件.
20.(1)解:由已知:對于 ,總有
,總有 ①成立
①成立
∴ (n ≥ 2)②
(n ≥ 2)②
①--②得
∴
∵ 均為正數,∴
均為正數,∴ (n ≥ 2)
(n ≥ 2)
∴數列 是公差為1的等差數列
又n=1時,
是公差為1的等差數列
又n=1時, ,
解得
,
解得 =1
=1
∴ .(
.( )
)
(2)證明:∵對任意實數 和任意正整數n,總有
和任意正整數n,總有 ≤
≤ .……6分
.……6分
∴

(3)解:由已知  ,
,

易得 
猜想 n≥2 時, 是遞減數列.
是遞減數列.
令
∵當
∴在 內
內 為單調遞減函數.
為單調遞減函數.
由 .
.
∴n≥2 時,  是遞減數列.即
是遞減數列.即 是遞減數列.
是遞減數列.
又 , ∴數列
, ∴數列 中的最大項為
中的最大項為 .
.
B.附加題部分
三、附加題部分:
21.(必做題)(本小題滿分12分)
解:(1)將 代入
代入 得
得 ,
,
由△ 可知
可知 ,
,
另一方面,弦長AB ,解得
,解得 ;
;
(2)當 時,直線為
時,直線為 ,要使得內接△ABC面積最大,
,要使得內接△ABC面積最大,
則只須使得 ,
,
即 ,即
,即 位于(4,4)點處.
位于(4,4)點處.
22.(必做題)(本小題滿分12分)
解:(1)分別記甲、乙、丙三個同學筆試合格為事件 、
、 、
、 ;
;
 表示事件“恰有一人通過筆試”
表示事件“恰有一人通過筆試”
則


(2)解法一:因為甲、乙、丙三個同學經過兩次考試后合格的概率均為 ,
,
所以 ,故
,故 .
.
解法二:分別記甲、乙、丙三個同學經過兩次考試后合格為事件 ,
,
則
所以 ,
,
 ,
, .
.
于是, .
.
23.(選做題)(本小題滿分8分)
證明:(1)過D點作DG∥BC,并交AF于G點,
∵E是BD的中點,∴BE=DE,
又∵∠EBF=∠EDG,∠BEF=∠DEG,
∴△BEF≌△DEG,則BF=DG,
∴BF:FC=DG:FC,
又∵D是AC的中點,則DG:FC=1:2,
則BF:FC=1:2;
(2)若△BEF以BF為底,△BDC以BC為底,
則由(1)知BF:BC=1:3,
又由BE:BD=1:2可知 :
: =1:2,其中
=1:2,其中 、
、 分別為△BEF和△BDC的高,
分別為△BEF和△BDC的高,
 則
則 ,則
,則 =1:5.
=1:5.
24.(選做題)(本小題滿分8分)
解:(1)消去參數 ,得直線
,得直線 的普通方程為
的普通方程為 ;-----------------------2分
;-----------------------2分
 即
即 ,
,
兩邊同乘以 得
得 ,
,
消去參數 ,得⊙
,得⊙ 的直角坐標方程為:
的直角坐標方程為:

(2)圓心 到直線
到直線 的距離
的距離 ,
,
所以直線 和⊙
和⊙ 相交.
相交.
25.(選做題)(本小題滿分8分)
解:MN = 
 =
= ,
,
即在矩陣MN變換下 ,
,
則 ,
,
即曲線 在矩陣MN變換下的函數解析式為
在矩陣MN變換下的函數解析式為 .
.
26.(選做題)(本小題滿分8分)
證明:(1)當 時,左邊=
時,左邊= ,
,
 時成立
時成立
(2)假設當 時成立,即
時成立,即
那么當 時,左邊
時,左邊



 時也成立
時也成立
根據(1)(2)可得不等式對所有的 都成立
都成立
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com