
題目列表(包括答案和解析)
(本小題滿分12分)![]() 學(xué)科網(wǎng)已知直四棱柱ABCD—A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F為棱BB1
學(xué)科網(wǎng)已知直四棱柱ABCD—A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F為棱BB1![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng) 的中點(diǎn),M為線段AC1的中點(diǎn).
的中點(diǎn),M為線段AC1的中點(diǎn).![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(1)求證:直線MF∥平面ABCD;![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(2)求證:平面AFC1⊥平面ACC1A1;![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(3)求平面AFC1與與平面ABCD所成二面角的大小.![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(本小題滿分12分)
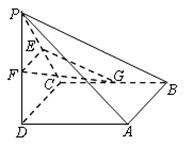
如圖所示,四棱錐 中,底面
中,底面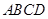 為正方形,
為正方形,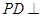 平面
平面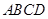 ,
,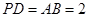 ,
,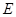 ,
,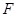 ,
,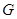 分別為
分別為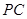 、
、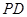 、
、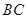 的中點(diǎn).
的中點(diǎn).
(1)求證:;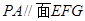 ;
;
(2)求三棱錐 的體積.
[來(lái)源:學(xué)*科*網(wǎng)]
的體積.
[來(lái)源:學(xué)*科*網(wǎng)]
(本小題滿分13分)如圖,四面體ABCD中,O是BD的中點(diǎn),
![]() ABD和
ABD和![]() BCD均為等邊三角形,AB=2,
BCD均為等邊三角形,AB=2,![]() 學(xué)科網(wǎng)AC=
學(xué)科網(wǎng)AC=![]() 。
。![]()
(1)求證:AO⊥平面BCD;![]() (2)求二面角A—BC—D的大小;
(2)求二面角A—BC—D的大小;
(3)求O點(diǎn)到平面ACD的距離。
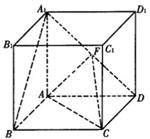
2.正方體.ABCD- ![]() 的棱長(zhǎng)為l,點(diǎn)F為
的棱長(zhǎng)為l,點(diǎn)F為![]() 的中點(diǎn).
的中點(diǎn).![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(I)證明: ![]() ∥平面AFC;.
∥平面AFC;.![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(Ⅱ)求二面角B-AF-一-C的大小.![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
![]() 學(xué)科網(wǎng)
學(xué)科網(wǎng)
(本小題滿分12分)
已知梯形ABCD中,AD∥BC,∠ABC ="∠BAD" = ,AB=BC=2AD=4,E、F分別是AB、CD上的點(diǎn),EF∥BC,AE = x,G是BC的中點(diǎn).沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF (如圖).
,AB=BC=2AD=4,E、F分別是AB、CD上的點(diǎn),EF∥BC,AE = x,G是BC的中點(diǎn).沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF (如圖).
(I)當(dāng)x=2時(shí),求證:BD⊥EG ;
(II)若以F、B、C、D為頂點(diǎn)的三棱錐的體積記為 ,
,
求 的最大值;
的最大值;
(III)當(dāng) 取得最大值時(shí),求二面角D-BF-C的余弦值.
取得最大值時(shí),求二面角D-BF-C的余弦值.
[來(lái)源:學(xué)科網(wǎng)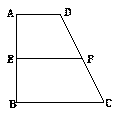 ZXXK
ZXXK ]
]
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com