日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

（本小題滿分14分）設是函數的一個極值點。

⑴求和的關系式并求的單調區間；

       ⑵設，若存在使得成立，求的取值范圍。

(本小題滿分14分)

某商店經銷一種奧運會紀念品，每件產品的成本為30元，并且每賣出一件產品需向稅務部門上交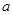元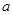（為常數，2≤a≤5 ）的稅收.設每件產品的售價為x元(35≤x≤41),根據市場調查,日銷售量與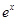(e為自然對數的底數)成反比例.已知每件產品的日售價為40元時，日銷售量為10件.

 (1)求該商店的日利潤L（x）元與每件產品的日售價x元的函數關系式；

 (2)當每件產品的日售價為多少元時，該商品的日利潤L（x）最大，并求出L（x）的最大值.

（本小題滿分14分）下圖是一個三角形數陣．從第二行起每一個數都等于它肩上兩個數的和，第行的第一個數為．

（Ⅰ）寫出與的遞推關系，并求；
（Ⅱ）求第行所有數的和；
（Ⅲ）求數陣中所有數的和；并證明：當時，．

(本小題滿分14分)

某工廠生產一種產品的成本費共由三部分組成：①原材料費每件50元；②職工工資支出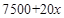元；③電力與機器保養等費用為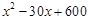元.其中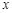是該廠生產這種產品的總件數。

（1）把每件產品的成本費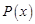(元)表示成產品件數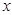的函數，并求每件產品的最低成本費；

（2）如果該廠生產的這種產品的數量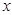不超過170件且能全部銷售，根據市場調查，每件產品的銷售價為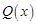（元），且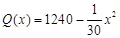，試問生產多少件產品，總利潤最高？并求出最高總利潤。（總利潤=總銷售額-總的成本）

（本小題滿分14分）

設是定義在[-1，1]上的偶函數，的圖象與的圖象關于直線對稱，且當x∈[ 2，3 ] 時， 2²²²3³．

（1）求的解析式；

（2）若在上為增函數，求的取值范圍；

（3）是否存在正整數，使的圖象的最高點落在直線上？若存在，求出的值；若不存在，請說明理由．