
題目列表(包括答案和解析)
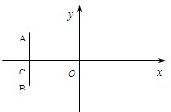 如圖,在直角坐標系中,O為坐標原點,直線AB⊥x軸與點C,|
如圖,在直角坐標系中,O為坐標原點,直線AB⊥x軸與點C,|| OC |
| CD |
| DO |
| KE |
| KF |
| OP |
| OE |
| OF |
如圖,在直角坐標系中,O為坐標原點,直線![]() ⊥x軸于點C,
⊥x軸于點C, ![]() ,
,![]() ,動點
,動點![]() 到直線
到直線![]() 的距離是它到點D的距離的2倍
的距離是它到點D的距離的2倍![]()
(I)求點![]() 的軌跡方程;
的軌跡方程;
(II)設點K為點![]() 的軌跡與x軸正半軸的交點,直線
的軌跡與x軸正半軸的交點,直線![]() 交點
交點![]() 的軌跡于
的軌跡于![]() 兩點(
兩點(![]() 與點K均不重合),且滿足
與點K均不重合),且滿足![]()
![]() 求直線EF在X軸上的截距;
求直線EF在X軸上的截距;
(Ⅲ)在(II)的條件下,動點![]() 滿足
滿足![]() ,求直線
,求直線![]() 的斜率的取值范圍
的斜率的取值范圍![]()
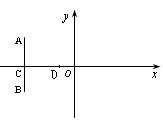
如圖,在直角坐標系中,O為坐標原點,直線![]() ⊥x軸與點C,
⊥x軸與點C, ![]() ,
,![]() ,動點
,動點![]() 到直線
到直線![]() 的距離是它到點D的距離的2倍。
的距離是它到點D的距離的2倍。
(I)求點![]() 的軌跡方程
的軌跡方程
(II)設點K為點![]() 的軌跡與x軸正半軸的交點,直線
的軌跡與x軸正半軸的交點,直線![]() 交點
交點![]() 的軌跡于
的軌跡于![]() 兩點(
兩點(![]() 與點K不重合),且滿足
與點K不重合),且滿足![]() .動點
.動點![]() 滿足
滿足![]() ,求直線
,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
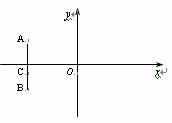
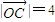 ,
,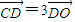 ,動點M到直線AB的距離是它到點D的距離的2倍.
,動點M到直線AB的距離是它到點D的距離的2倍.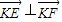 .動點P滿足
.動點P滿足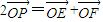 ,求直線KP的斜率的取值范圍.
,求直線KP的斜率的取值范圍.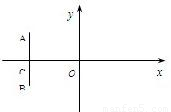
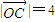 ,
, ,動點M到直線AB的距離是它到點D的距離的2倍.
,動點M到直線AB的距離是它到點D的距離的2倍.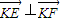 .動點P滿足
.動點P滿足 ,求直線KP的斜率的取值范圍.
,求直線KP的斜率的取值范圍.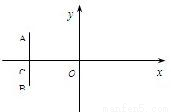
一、1 B 2 D
二、13、3 14、-160 15、.files/image211.gif) 16、
16、.files/image213.gif)
三、17、解: (1).files/image215.gif)
.files/image002.gif) ……
3分
……
3分
.files/image217.gif)
.files/image133.gif) 的最小正周期為
的最小正周期為.files/image219.gif)
.files/image002.gif) …………………
5分
…………………
5分
(2) .files/image221.gif) ,
………………… 7分
,
………………… 7分
.files/image223.gif) ………………… 10分
………………… 10分
.files/image217.gif)
.files/image225.gif)
.files/image002.gif) …………………
11分
…………………
11分
.files/image217.gif) 當
當.files/image135.gif) 時,函數
時,函數.files/image133.gif) 的最大值為1,最小值
的最大值為1,最小值.files/image227.gif)
.files/image002.gif) ………… 12分
………… 12分
18、(I)解:設這箱產品被用戶拒絕接收事件為A,被接收為.files/image229.gif) ,則由對立事件概率公式
,則由對立事件概率公式
.files/image231.gif) 得:
得:.files/image233.gif)
即這箱產品被用戶拒絕接收的概率為.files/image235.gif)
.files/image002.gif) …………
6分
…………
6分
(II).files/image237.gif)
.files/image239.gif) ………… 10分
………… 10分
.files/image241.gif)
1
2
3
P
.files/image243.gif)
.files/image245.gif)
.files/image247.gif)
…………11分
∴ E.files/image241.gif) =
=.files/image250.gif) …………12分
…………12分
19、解法一:
.files/image252.jpg) (Ⅰ)連結B
(Ⅰ)連結B.files/image254.gif) 于O,則O是B
于O,則O是B.files/image254.gif) C的中點,連結DO。
C的中點,連結DO。
∵在△A.files/image257.gif) C中,O、D均為中點,
C中,O、D均為中點,
∴A.files/image257.gif) ∥DO …………………………2分
∥DO …………………………2分
∵A.files/image257.gif)
.files/image259.gif) 平面B
平面B.files/image139.gif) D,DO
D,DO.files/image262.gif) 平面B
平面B.files/image139.gif) D,
D,
∴A.files/image257.gif) ∥平面B
∥平面B.files/image139.gif) D。…………………4分
D。…………………4分
(Ⅱ)設正三棱柱底面邊長為2,則DC = 1。
∵∠.files/image139.gif) DC = 60°,∴C
DC = 60°,∴C.files/image139.gif) =
= .files/image264.gif) 。
。
作DE⊥BC于E。
∵平面BC.files/image139.gif) ⊥平面ABC,
⊥平面ABC,
∴DE⊥平面BC.files/image139.gif)
.files/image257.gif)
作EF⊥B.files/image139.gif) 于F,連結DF,則 DF⊥B
于F,連結DF,則 DF⊥B.files/image139.gif)
∴∠DFE是二面角D-B.files/image139.gif) -C的平面角……………………………………8分
-C的平面角……………………………………8分
在Rt△DEC中,DE=.files/image268.gif)
在Rt△BFE中,EF =
BE?sin.files/image270.gif)
∴在Rt△DEF中,tan∠DFE = .files/image272.gif)
.files/image274.gif) ∴二面角D-B
∴二面角D-B.files/image139.gif) -C的大小為arctan
-C的大小為arctan.files/image277.gif) ………………12分
………………12分
解法二:以AC的中D為原點建立坐標系,如圖,
設| AD | = 1∵∠.files/image139.gif) DC =60°∴| C
DC =60°∴| C.files/image139.gif) |
=
|
= .files/image264.gif) 。
。
則A(1,0,0),B(0,.files/image264.gif) ,0),C(-1,0,0),
,0),C(-1,0,0),
.files/image282.gif) (1,0
(1,0.files/image264.gif) ),
),.files/image285.gif) ,
,.files/image287.gif)
(Ⅰ)連結.files/image257.gif) C交B
C交B.files/image290.gif) 于O是
于O是.files/image257.gif) C的中點,連結DO,則
O
C的中點,連結DO,則
O.files/image293.gif) .
. .files/image295.gif) =
=.files/image297.gif)
∵A.files/image257.gif)
.files/image259.gif) 平面B
平面B.files/image290.gif) D,
D,
∴A.files/image257.gif) ∥平面B
∥平面B.files/image290.gif) D.……………………………………………………………4分
D.……………………………………………………………4分
(Ⅱ).files/image303.gif) =(-1,0,
=(-1,0,.files/image264.gif) ),
),.files/image306.gif)
設平面B.files/image290.gif) D的法向量為n = ( x , y , z ),則
D的法向量為n = ( x , y , z ),則.files/image309.gif)
即.files/image311.gif) 則有
則有.files/image313.gif) = 0令z = 1
= 0令z = 1
則n = (.files/image264.gif) ,0,1)…………………………………………………………8分
,0,1)…………………………………………………………8分
設平面BC.files/image139.gif)
.files/image257.gif) 的法向量為m = ( x′
,y′,z′)
的法向量為m = ( x′
,y′,z′)
|