
題目列表(包括答案和解析)
在 中,
中,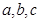 ,分別是角
,分別是角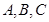 所對邊的長,
所對邊的長,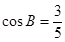 ,且
,且
(1)求 的面積;
的面積;
(2)若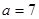 ,求角C.
,求角C.
【解析】第一問中,由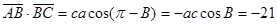 又∵
又∵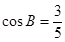 ∴
∴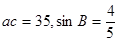 ∴
∴ 的面積為
的面積為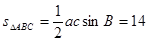
第二問中,∵a =7 ∴c=5由余弦定理得: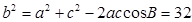 得到b的值,然后又由余弦定理得:
得到b的值,然后又由余弦定理得: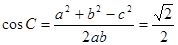
又C為內角 ∴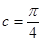
解:(1)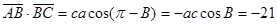 ………………2分
………………2分
又∵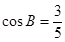 ∴
∴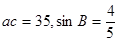 ……………………4分
……………………4分
∴ 的面積為
的面積為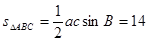 ……………………6分
……………………6分
(2)∵a =7 ∴c=5 ……………………7分
由余弦定理得: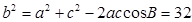
∴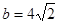 ……………………9分
……………………9分
又由余弦定理得: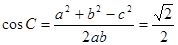
又C為內角 ∴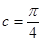 ……………………12分
……………………12分
另解:由正弦定理得: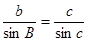 ∴
∴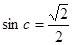 又
又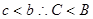 ∴
∴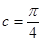
已知向量 =(
=( ),
), =(
=(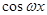 ,
,
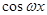 ),其中(
),其中(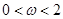 ).函數
).函數 ,其圖象的一條對稱軸為
,其圖象的一條對稱軸為 .
.
(I)求函數 的表達式及單調遞增區間;
的表達式及單調遞增區間;
(Ⅱ)在△ABC中,a、b、c分別為角A、B、C的對邊,S為其面積,若 =1,b=l,S△ABC=
=1,b=l,S△ABC= ,求a的值.
,求a的值.
【解析】第一問利用向量的數量積公式表示出
 ,然后利用
,然后利用 得到
得到 ,從而得打解析式。第二問中,利用第一問的結論,表示出A,結合正弦面積公式和余弦定理求解a的值。
,從而得打解析式。第二問中,利用第一問的結論,表示出A,結合正弦面積公式和余弦定理求解a的值。
解:因為

由余弦定理得 ,……11分故
,……11分故
如圖 是單位圓
是單位圓 上的點,
上的點, 分別是圓
分別是圓 與
與 軸的兩交點,
軸的兩交點, 為正三角形.
為正三角形.

(1)若 點坐標為
點坐標為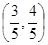 ,求
,求 的值;
的值;
(2)若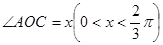 ,四邊形
,四邊形 的周長為
的周長為 ,試將
,試將 表示成
表示成 的函數,并求出
的函數,并求出 的最大值.
的最大值.
【解析】第一問利用設
∵ A點坐標為 ∴
∴  ,
,
(2)中 由條件知 AB=1,CD=2 ,
在 中,由余弦定理得
中,由余弦定理得 
∴ 
∵  ∴
∴  ,
,
∴ 當 時,即
當
時,即
當 時 , y有最大值5. .
時 , y有最大值5. .
已知△ 的內角
的內角 所對的邊分別為
所對的邊分別為 且
且 .
.
(1)
若 , 求
, 求 的值;
的值;
(2)
若△ 的面積
的面積 求
求 的值.
的值.
【解析】本小題主要考查正弦定理、余弦定理、同角三角函數的基本關系等基礎知識,考查運算求解能力。第一問中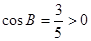 ,得到正弦值
,得到正弦值 ,再結合正弦定理可知,
,再結合正弦定理可知, ,得到
,得到 (2)中
(2)中 即
即 所以c=5,再利用余弦定理
所以c=5,再利用余弦定理 ,得到b的值。
,得到b的值。
解: (1)∵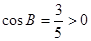 , 且
, 且 , ∴
, ∴  . 由正弦定理得
. 由正弦定理得 , ∴
, ∴ .
.
(2)∵ ∴
∴ . ∴c=5
. ∴c=5
由余弦定理得 ,
,
∴ 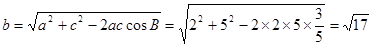
在△ABC中,內角A、B、C所對邊的邊長分別是a、b、c,已知c=2,C= .
.
(Ⅰ)若△ABC的面積等于 ,求a、b;
,求a、b;
(Ⅱ)若 ,求△ABC的面積.
,求△ABC的面積.
【解析】第一問中利用余弦定理及已知條件得 又因為△ABC的面積等于
又因為△ABC的面積等于 ,所以
,所以 ,得
,得 聯立方程,解方程組得
聯立方程,解方程組得 .
.
第二問中。由于 即為即
即為即 .
.
當 時,
時,
 ,
,  ,
,  ,
,
 所以
所以 當
當 時,得
時,得 ,由正弦定理得
,由正弦定理得 ,聯立方程組
,聯立方程組 ,解得
,解得 ,得到
,得到 。
。
解:(Ⅰ) (Ⅰ)由余弦定理及已知條件得 ,………1分
,………1分
又因為△ABC的面積等于 ,所以
,所以 ,得
,得 ,………1分
,………1分
聯立方程,解方程組得 .
……………2分
.
……………2分
(Ⅱ)由題意得
 ,
,
即 .
…………2分
.
…………2分
當 時,
時,
 ,
,  ,
,  ,
,
 ……1分
……1分
所以 ………………1分
………………1分
當 時,得
時,得 ,由正弦定理得
,由正弦定理得 ,聯立方程組
,聯立方程組
 ,解得
,解得 ,
, ;
所以
;
所以
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com