
題目列表(包括答案和解析)
| Sn |
| 1 |
| 4 |
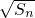 是
是 與(an+1)2的等比中項,求an及bn通項;
與(an+1)2的等比中項,求an及bn通項; 是
是 與(an+1)2的等比中項,求an及bn通項;
與(an+1)2的等比中項,求an及bn通項;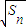 是
是 與(an+1)2的等比中項,求an及bn通項;
與(an+1)2的等比中項,求an及bn通項;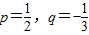 ,求b3;
,求b3;一、填空題:本大題共14小題,每小題5分,共計70分.
1.--數學.files/image175.gif) 2.
2.--數學.files/image177.gif) 3.0 4.充分而不必要 5.
3.0 4.充分而不必要 5.--數學.files/image179.gif) 6.2
6.2
7.--數學.files/image181.gif) 8.5
9.
8.5
9.--數學.files/image183.gif) 10.1.5
11.
10.1.5
11.
13.14.--數學.files/image185.gif)
二、解答題:本大題共6小題,共計90分.
15.(本小題滿分14分)
(1)--數學.files/image187.gif) =
=--數學.files/image189.gif) =
=--數學.files/image191.gif) ……………………………………2分
……………………………………2分
=--數學.files/image193.gif) =
=--數學.files/image195.gif) ……………………………………………………………………………………………4分
……………………………………………………………………………………………4分
--數學.files/image197.gif)
--數學.files/image199.gif) ……………………………………………………………………………6分
……………………………………………………………………………6分
(2)--數學.files/image201.gif) =
=--數學.files/image203.gif) =
=--數學.files/image205.gif)
=--數學.files/image207.gif) =
=--數學.files/image209.gif) …………………………………………………………………………9分
…………………………………………………………………………9分
由--數學.files/image211.gif) ,得
,得--數學.files/image213.gif) ………………………………………………………………………10分
………………………………………………………………………10分
--數學.files/image215.gif)
--數學.files/image217.gif) ……………………………………………………………………12分
……………………………………………………………………12分
--數學.files/image219.gif) 當
當--數學.files/image221.gif) , 即
, 即--數學.files/image223.gif) 時,
時,--數學.files/image211.gif) …………………………………………………………14分
…………………………………………………………14分
16.(本小題滿分14分)
(1)在梯形--數學.files/image226.gif) 中,
中,--數學.files/image228.gif) ,
,
--數學.files/image230.gif)
--數學.files/image232.gif)
--數學.files/image219.gif) 四邊形
四邊形--數學.files/image226.gif) 是等腰梯形,
是等腰梯形,
且--數學.files/image235.gif)
--數學.files/image237.gif)
--數學.files/image239.gif) …………………3分
…………………3分
又--數學.files/image241.gif) 平面
平面--數學.files/image243.gif) 平面
平面--數學.files/image226.gif) ,交線為
,交線為--數學.files/image036.gif) ,
,
--數學.files/image246.gif) 平面
平面--數學.files/image248.gif) …………………………………………………6分
…………………………………………………6分
(2)當--數學.files/image250.gif) 時,
時,--數學.files/image252.gif) 平面
平面--數學.files/image254.gif) ,………………………7分
,………………………7分
在梯形--數學.files/image226.gif) 中,設
中,設--數學.files/image257.gif) ,連接
,連接--數學.files/image259.gif) ,則
,則--數學.files/image261.gif) …………………………………8分
…………………………………8分
--數學.files/image263.gif) ,而
,而--數學.files/image265.gif)
--數學.files/image267.gif) ,……………………………………………10分
,……………………………………………10分
--數學.files/image269.gif) ,
,--數學.files/image219.gif) 四邊形
四邊形--數學.files/image272.gif) 是平行四邊形,
是平行四邊形,--數學.files/image274.gif) …………………………………………12分
…………………………………………12分
又--數學.files/image276.gif) 平面
平面--數學.files/image254.gif) ,
,--數學.files/image279.gif) 平面
平面--數學.files/image254.gif)
--數學.files/image282.gif) 平面
平面--數學.files/image254.gif) …………………………………………14分
…………………………………………14分
18.(本小題滿分16分)
(1)設橢圓--數學.files/image133.gif) 的焦距為
的焦距為
則其右準線方程為x=--數學.files/image285.gif) ,且F1(-c, 0), F2(c, 0). ……………2分
,且F1(-c, 0), F2(c, 0). ……………2分
設M--數學.files/image287.gif) ,
,
則--數學.files/image289.gif) =
=--數學.files/image291.gif)
--數學.files/image293.gif) . ………………………4分
. ………………………4分
因為--數學.files/image136.gif) ,所以
,所以--數學.files/image295.gif) ,即
,即--數學.files/image297.gif) .
.
于是--數學.files/image299.gif) ,故∠MON為銳角.
,故∠MON為銳角.
所以原點O在圓C外. ………………………7分
(2)因為橢圓的離心率為--數學.files/image138.gif) ,所以a=
,所以a=
于是M --數學.files/image301.gif) ,且
,且--數學.files/image303.gif) …………………9分
…………………9分
MN2=(y1-y2)2=y12+y22-2y1y2--數學.files/image305.gif) . ………… 12分
. ………… 12分
當且僅當 y1=-y2=--數學.files/image307.gif) 或y2=-y1=
或y2=-y1=--數學.files/image307.gif) 時取“=”號, ……………… 14分
時取“=”號, ……………… 14分
所以(MN)min=
故所求的橢圓方程是--數學.files/image309.gif) .
………………… 16分
.
………………… 16分
19.(本小題滿分16分)
(1)函數的定義域為--數學.files/image311.gif)
--數學.files/image313.gif) .…………………………………1分
.…………………………………1分
由--數學.files/image315.gif) 得
得--數學.files/image317.gif) ;…………………………………………………………………………………………2分
;…………………………………………………………………………………………2分
由--數學.files/image319.gif) 得
得--數學.files/image321.gif) ,……………………………………………………………………………………3分
,……………………………………………………………………………………3分
則增區間為--數學.files/image323.gif) ,減區間為
,減區間為--數學.files/image325.gif) . ………………………………………………………………………4分
. ………………………………………………………………………4分
(2)令--數學.files/image327.gif) 得
得--數學.files/image329.gif) ,由(1)知
,由(1)知--數學.files/image144.gif) 在
在--數學.files/image332.gif) 上遞減,在
上遞減,在--數學.files/image334.gif) 上遞增, …………6分
上遞增, …………6分
由--數學.files/image336.gif)
--數學.files/image338.gif) ,且
,且--數學.files/image340.gif) ,………………………………………………8分
,………………………………………………8分
--數學.files/image342.gif) 時,
時,--數學.files/image144.gif) 的最大值為
的最大值為--數學.files/image345.gif) ,故
,故--數學.files/image347.gif) 時,不等式
時,不等式--數學.files/image349.gif) 恒成立. …………10分
恒成立. …………10分
(3)方程--數學.files/image351.gif) 即
即--數學.files/image353.gif) .記
.記--數學.files/image355.gif) ,則
,則
--數學.files/image357.gif) .由
.由--數學.files/image359.gif) 得
得--數學.files/image361.gif) ;由
;由--數學.files/image363.gif) 得
得--數學.files/image365.gif) .
.
所以--數學.files/image367.gif) 在
在--數學.files/image369.gif) 上遞減;在
上遞減;在--數學.files/image371.gif) 上遞增.
上遞增.
而--數學.files/image373.gif) ,
,--數學.files/image375.gif) ……………………………………12分
……………………………………12分
所以,當--數學.files/image377.gif) 時,方程無解;
時,方程無解;
當--數學.files/image379.gif) 時,方程有一個解;
時,方程有一個解;
當--數學.files/image381.gif) 時,方程有兩個解;
時,方程有兩個解;
當--數學.files/image383.gif) 時,方程有一個解;
時,方程有一個解;
當--數學.files/image385.gif) 時,方程無解. ………………………………………………………………………………14分
時,方程無解. ………………………………………………………………………………14分
綜上所述,--數學.files/image387.gif) 時,方程無解;
時,方程無解;
--數學.files/image389.gif) 或
或--數學.files/image383.gif) 時,方程有唯一解;
時,方程有唯一解;
--數學.files/image392.gif) 時,方程有兩個不等的解. ……………………………………………16分
時,方程有兩個不等的解. ……………………………………………16分
20.(本小題滿分16分)
(1)因為第一行數組成的數列{A1j}(j=1,2,…)是以1為首項,公差為3的等差數列,
所以A1 j=1+(j-1)×3=3 j-2,
第二行數組成的數列{A2j}(j=1,2,…)是以4為首項,公差為4的等差數列,
所以A2 j=4+(j-1)×4=4 j. ……………………2分
所以A2 j-A1 j=4 j-(3 j-2)=j+2,
所以第j列數組成的數列{ Aij}(i=1,2,…)是以3 j-2為首項,公差為 j+2的等差數列,
所以Aij=3 j-2+(i-1) ×(j+2) =ij+2i+2j-4=(i+3) (j+2) 8. …………5分
故Aij+8=(i+3) (j+2)是合數.
所以當--數學.files/image394.gif) =8時,對任意正整數i、j,
=8時,對任意正整數i、j,--數學.files/image160.gif) 總是合數 …………………6分
總是合數 …………………6分
(2) (反證法)假設存在k、m,--數學.files/image396.gif) ,使得
,使得--數學.files/image398.gif) 成等比數列,
成等比數列,
即--數學.files/image400.gif) ………………………7分
………………………7分
∵bn=Ann =(n+2)2-4
∴--數學.files/image402.gif)
得--數學.files/image404.gif) ,
,
即--數學.files/image406.gif) , …………………10分
, …………………10分
又∵--數學.files/image396.gif) ,且k、m∈N,∴k≥2、m≥3,
,且k、m∈N,∴k≥2、m≥3,--數學.files/image408.gif)
∴--數學.files/image410.gif) ,這與
,這與--數學.files/image412.gif) ∈Z矛盾,所以不存在正整數k和m
∈Z矛盾,所以不存在正整數k和m--數學.files/image164.gif) ,使得
,使得--數學.files/image166.gif) 成等比數列.……………………12分
成等比數列.……………………12分
(3)假設存在滿足條件的--數學.files/image414.gif) ,那么
,那么--數學.files/image416.gif)
即--數學.files/image418.gif) . …………………… 14分
. …………………… 14分
不妨令--數學.files/image420.gif) 得
得--數學.files/image422.gif)
所以存在--數學.files/image424.gif) 使得
使得--數學.files/image171.gif) 成等差數列.
…………………… 16分
成等差數列.
…………………… 16分
(注:第(3)問中數組--數學.files/image426.gif) 不唯一,例如
不唯一,例如--數學.files/image428.gif) 也可以)
也可以)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com