
題目列表(包括答案和解析)
(本題滿分16分)已知二次函數f (x) = x2 ??ax + a (x∈R)同時滿足:①不等式 f (x) ≤ 0的解集有且只有一個元素;②在定義域內存在0 < x1 < x2,使得不等式f (x1) > f (x2)成立.設數列{an}的前 n 項和Sn = f (n).(1)求函數f (x)的表達式;(2)求數列{an}的通項公式;(3)在各項均不為零的數列{cn}中,若ci·ci+1 < 0,則稱ci,ci+1為這個數列{cn}一對變號項.令cn = 1 ?? (n為正整數),求數列{cn}的變號項的對數.
(本題滿分12分) 已知二次函數 滿足
滿足 ,且關于
,且關于 的方程
的方程 的兩實數根分別在區間(-3,-2),(0,1)內。
的兩實數根分別在區間(-3,-2),(0,1)內。
(Ⅰ)求實數 的取值范圍;
的取值范圍;
(Ⅱ)若函數 在區間(-1-
在區間(-1- ,1-
,1- )上具有單調性,求實數C的取值范圍
)上具有單調性,求實數C的取值范圍
(本題滿分12分)
已知二次函數 滿足
滿足 且
且 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)當 時,不等式:
時,不等式: 恒成立,求實數
恒成立,求實數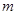 的范圍.
的范圍.
(.(本題滿分12分)
已知二次函數 和“偽二次函數”
和“偽二次函數”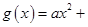
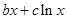 (
(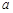 、
、 、
、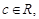
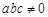 ),
),
(I)證明:只要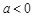 ,無論
,無論 取何值,函數
取何值,函數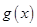 在定義域內不可能總為增函數;
在定義域內不可能總為增函數;
(II)在二次函數 圖象上任意取不同兩點
圖象上任意取不同兩點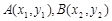 ,線段
,線段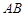 中點的橫坐標為
中點的橫坐標為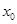 ,記直線
,記直線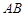 的斜率為
的斜率為 ,
,
(i)求證: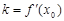 ;
;
(ii)對于“偽二次函數”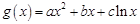 ,是否有(i)同樣的性質?證明你的結論.
,是否有(i)同樣的性質?證明你的結論.
(本題滿分12分)
已知二次函數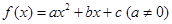 滿足
滿足 且
且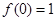 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)當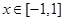 時,不等式:
時,不等式: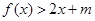 恒成立,求實數
恒成立,求實數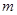 的范圍.
的范圍.
一、填空題:本大題共14小題,每小題5分,共70分.
1. 2.
2. 3.
3. 4.
4. 5.1 6.
5.1 6. 7.
7. 8.
8. 9.16 10.8
11.
9.16 10.8
11. 12.
12. 13.
13. 14. ①③
14. ①③
二、解答題:本大題共6小題,共90分.
15.(1)設集合 中的點
中的點 為事件
為事件 , 區域
, 區域 的面積為
的面積為 36, 區域
36, 區域 的面積為
的面積為 18
18

 .
.
(2)設點 在集合
在集合 為事件
為事件 , 甲、乙兩人各擲一次骰子所得的點數為36個,其中在集合
, 甲、乙兩人各擲一次骰子所得的點數為36個,其中在集合 中的點有21個,故
中的點有21個,故 .
.
16.(1)由4sinB ? sin2 + cos2B = 1 +
+ cos2B = 1 + 得:
得:
 ,
, 

 或
或 .
.
(2)法1: 為銳角
為銳角 

由已知得: , 角
, 角 為銳角
為銳角  可得:
可得:
由正弦定理 得:
得: .
.
法2:由 得:
得: , 由余弦定理知:
, 由余弦定理知:
即:


 .
.
17.(1)證明:連接 ,取
,取 中點
中點 ,連接
,連接 .
.
 在等腰梯形
在等腰梯形 中,
中, ∥
∥ ,AB=AD,
,AB=AD, ,E是BC的中點
,E是BC的中點
 與
與 都是等邊三角形
都是等邊三角形 
 平面
平面
 平面
平面
 平面
平面
 .
.
(2)證明:連接 交
交 于點
于點 ,連接
,連接
 ∥
∥ ,且
,且 =
=
 四邊形
四邊形 是平行四邊形
是平行四邊形  是線段
是線段 的中點
的中點
 是線段
是線段 的中點
的中點  ∥
∥
 平面
平面
 平面
平面 .
.
(3) 與平面
與平面 不垂直.
不垂直.
證明:假設 平面
平面 , 則
, 則
 平面
平面

 ,
, 平面
平面
 平面
平面
 ,這與
,這與 矛盾
矛盾
 與平面
與平面 不垂直.
不垂直.
18.(1)設橢圓的標準方程為
依題意得: ,得
,得 ∴
∴ 所以,橢圓的標準方程為
所以,橢圓的標準方程為 .
.
(2)設過點 的直線方程為:
的直線方程為: ,代入橢圓方程
,代入橢圓方程 得;
得;
 (*)
(*)
依題意得: ,即
,即
得: ,且方程的根為
,且方程的根為

當點 位于
位于 軸上方時,過點
軸上方時,過點 與
與 垂直的直線與
垂直的直線與 軸交于點
軸交于點 ,
,
直線 的方程是:
的方程是: ,
, 
所求圓即為以線段DE為直徑的圓,故方程為:
同理可得:當點 位于
位于 軸下方時,圓的方程為:
軸下方時,圓的方程為: .
.
(3)設 ,
, 由
由 =
= 得:
得: ,代入
,代入
 (**) 要證
(**) 要證 =
= ,即證
,即證
由方程組(**)可知方程組(1)成立,(2)顯然成立.∴ =
=
19..解(1) 的解集有且只有一個元素,
的解集有且只有一個元素,

當a=4時,函數 上遞減
上遞減
故存在 ,使得不等式
,使得不等式 成立
成立
當a=0時,函數 上遞增
上遞增
故不存在 ,使得不等式
,使得不等式 成立
成立
綜上,得a=4, …………………………5分
…………………………5分
(2)由(1)可知
當n=1時,
當 時,
時,



(3) ,
,






 …
…
+
= +
+ >
>
>
20解:(1)由 的定義可知,
的定義可知, (對所有實數
(對所有實數 )等價于
)等價于
 (對所有實數
(對所有實數 )這又等價于
)這又等價于 ,即
,即
 對所有實數
對所有實數 均成立. (*)
均成立. (*)
由于 的最大值為
的最大值為 ,
,
故(*)等價于 ,即
,即 ,這就是所求的充分必要條件
,這就是所求的充分必要條件
(2)分兩種情形討論
(i)當 時,由(1)知
時,由(1)知 (對所有實數
(對所有實數 )
)
 則由
則由 及
及 易知
易知 ,
,
再由 的單調性可知,
的單調性可知,
函數 在區間
在區間 上的單調增區間的長度
上的單調增區間的長度
為 (參見示意圖1)
(參見示意圖1)
(ii) 時,不妨設
時,不妨設 ,則
,則 ,于是
,于是
當 時,有
時,有 ,從而
,從而 ;
;
當 時,有
時,有
從而  ;
;
當 時,
時, ,及
,及 ,由方程
,由方程
 解得
解得 圖象交點的橫坐標為
圖象交點的橫坐標為
 ⑴
⑴
顯然 ,
,
這表明 在
在 與
與 之間。由⑴易知
之間。由⑴易知

綜上可知,在區間 上,
上, (參見示意圖2)
(參見示意圖2)
故由函數 及
及 的單調性可知,
的單調性可知, 在區間
在區間 上的單調增區間的長度之和為
上的單調增區間的長度之和為 ,由于
,由于 ,即
,即 ,得
,得
 ⑵
⑵
故由⑴、⑵得 
綜合(i)(ii)可知, 在區間
在區間 上的單調增區間的長度和為
上的單調增區間的長度和為 。
。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com