
題目列表(包括答案和解析)
用![]() 表示不大于
表示不大于![]() 的最大整數.令集合
的最大整數.令集合![]() ,對任意
,對任意![]() 和
和![]() ,定義
,定義![]() ,集合
,集合![]() ,并將集合
,并將集合![]() 中的元素按照從小到大的順序排列,記為數列
中的元素按照從小到大的順序排列,記為數列![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的值;
的值;
(Ⅲ)求證:在數列![]() 中,不大于
中,不大于![]() 的項共有
的項共有![]() 項.
項.
6
|
| [ |
| 2 |
| 3 |
| 1 |
| 3 |
()(本小題滿分12分)貴陽六中織高二年級4個班的學生到益佰制藥廠、貴陽鋼廠、貴陽輪胎廠進行社會實踐,規定每個班只能在這3個廠中任選擇一個,假設每個班選擇每個廠的概率是等可能的。(Ⅰ)求3個廠都有班級選擇的概率;(Ⅱ)用![]() 表示有班級選擇的廠的個數,求隨機變量
表示有班級選擇的廠的個數,求隨機變量![]() 的概率分布及數學期望
的概率分布及數學期望![]() 。
。
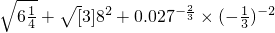 .
.6
|
| [ |
| 2 |
| 3 |
| 1 |
| 3 |
(二十三)
【解題思路】:設f(x)的二次項系數為m,其圖象上兩點為(1-x, )、B(1+x,
)、B(1+x, )因為
)因為 ,
, ,所以
,所以 ,由x的任意性得f(x)的圖象關于直線x=1對稱, ………………………………………………………………(2分)
,由x的任意性得f(x)的圖象關于直線x=1對稱, ………………………………………………………………(2分)
∵  ,
, ,
, ,
,
 ,
, ,
,
 ,………………………………(4分)
,………………………………(4分)
∴ 當 時,∵f(x)在x≥1內是增函數,
時,∵f(x)在x≥1內是增函數,





 ,
, .
.
∵  , ∴
, ∴  .………………………………………………(8分)
.………………………………………………(8分)
當 時,∵f(x)在x≥1內是減函數.
時,∵f(x)在x≥1內是減函數.
同理可得 或
或 ,
, .………………………………………(11分)
.………………………………………(11分)
綜上: 的解集是當
的解集是當 時,為
時,為
當 時,為
時,為 ,或
,或 .…………………………(12分)
.…………………………(12分)
【試題評析】:本小題主要考查最簡單三角不等式的解法等基本知識,涉及到分類討論、二次函數的對稱性、向量的數量積、函數的單調性等基本知識和方法的綜合運用,考查運算能力及邏輯思維能力。
18.(理)【解題思路】:(1)設甲隊在第五場比賽后獲得冠軍為事件M,則第五場比賽甲隊獲勝,前四場比賽甲隊獲勝三場,
依題意得 .……………………………(6分)
.……………………………(6分)
(2)設甲隊獲得冠軍為事件E,則E包含第四、第五、第六、第七場獲得冠軍四種情況,且它們彼此互斥.
∴  .
.
………………………………………………………………(12分)
【試題評析】:考查互斥事件有一個發生的概率,相互獨立事件同時發生的概率,n次獨立重復實驗恰好k次發生的概率。考查邏輯思維能力,要求考生具有較強的辨別雷同信息的能力。
19.【解題思路】:解法一:(1)取PC中點M,連結ME、MF,則MF∥CD,MF= CD,又AE∥CD,AE=
CD,又AE∥CD,AE= CD,∴AE∥MF,且AE=MF,∴四邊形AFME是平行四邊形,∴AF∥EM,∵AF
CD,∴AE∥MF,且AE=MF,∴四邊形AFME是平行四邊形,∴AF∥EM,∵AF 平面PCE,∴AF∥平面PCE. …………………………………(4分)
平面PCE,∴AF∥平面PCE. …………………………………(4分)
(2)∵PA⊥平面ABCD,CD⊥AD. ∴CD⊥PD,∴∠PDA是二面角P-CD-B的平面角,即∠PDA=45°, ………………………………………………………………(6分)
∴△PAD是等腰直角三角形,∴AF⊥PD,又AF⊥CD,∴AF⊥平面PCD,而EM∥AF,∴EM⊥平面PCD. 又EM 平面PEC,∴面PEC⊥面PCD. 在平面PCD內過F作FH⊥PC于H,則FH就是點F到平面PCE的距離. …………………………………(10分)
平面PEC,∴面PEC⊥面PCD. 在平面PCD內過F作FH⊥PC于H,則FH就是點F到平面PCE的距離. …………………………………(10分)
由已知,PD= ,PF=
,PF= ,PC=
,PC= ,△PFH∽△PCD,∴
,△PFH∽△PCD,∴ ,
,
∴FH= .
………………………………………………………………(12分)
.
………………………………………………………………(12分)
解法二:(1)取PC中點M,連結EM,



 =
= +
+
 =
= ,∴AF∥EM,又EM
,∴AF∥EM,又EM 平面PEC,AF
平面PEC,AF 平面PEC,∴AF∥平面PEC. ………………………………………………(4分)
平面PEC,∴AF∥平面PEC. ………………………………………………(4分)
 (2)以A為坐標原點,分別以
(2)以A為坐標原點,分別以 所在直線為x、y、z
所在直線為x、y、z
軸建立坐標系. ∵PA⊥平面ABCD,CD⊥AD,∴CD⊥PD,
∴∠PDA是二面角P-CD-B的平面角,即∠PDA=45°. ……(6分)
∴A(0, 0, 0), P(0, 0, 2), D(0, 2, 0), F(0, 1, 1), E , C(3, 2, 0),設平面PCE的法向量為
, C(3, 2, 0),設平面PCE的法向量為 =(x, y, z),則
=(x, y, z),則 ⊥
⊥ ,
, ⊥
⊥ ,而
,而 =(-
=(- ,0,2),
,0,2),
 =(
=( ,2,0),∴-
,2,0),∴- x+2z=0,且
x+2z=0,且 x+2y=0,解得y=-
x+2y=0,解得y=- x,z=
x,z= x. 取x=4
x. 取x=4
得 =(4, -3, 3),………………………………………………………………(10分)
=(4, -3, 3),………………………………………………………………(10分)
又 =(0,1,-1),
=(0,1,-1),
故點F到平面PCE的距離為d= .…………(12分)
.…………(12分)
【試題評析】:本小題主要考查直線與平面的位置關系等基本知識,是否利用空間向量供考生選擇。考查空間想象能力、邏輯推理能力和運算能力
(二十四)
17. 解:(1) 設 ,則
,則 …………………1分
…………………1分
 …………………2分
…………………2分
又 是奇函數,所以
是奇函數,所以 …………………3分
…………………3分

 =
= ……4分
……4分
………………5分
 是[-1,1]上增函數………………6分
是[-1,1]上增函數………………6分
(2) 是[-1,1]上增函數,由已知得:
是[-1,1]上增函數,由已知得: …………7分
…………7分
等價于 …………10分
…………10分
解得: ,所以
,所以 …………12分
…………12分

 二次函數
二次函數 在
在 上遞減………………………12分
上遞減………………………12分
故 時,
時,
 ……………………13分
……………………13分
 ,
, …………………………14分
…………………………14分
(二十五)
16.解: 由題意,得 為銳角,
為銳角, , 3分
, 3分
 , 6分
, 6分
由正弦定理得  , 9分
, 9分

 . 12分
. 12分
17.(本題滿分12分)
有紅藍兩粒質地均勻的正方體形狀骰子,紅色骰子有兩個面是8,四個面是2,藍色骰子有三個面是7,三個面是1,兩人各取一只骰子分別隨機擲一次,所得點數較大者獲勝.
(1)分別求出兩只骰子投擲所得點數的分布列及期望;
(2)求投擲藍色骰子者獲勝的概率是多少?
17.解:(1)設紅色骰子投擲所得點數為 ,其分布如下:
,其分布如下:

8
2
P

|