
題目列表(包括答案和解析)
(本小題滿分12分)
△ABC中,a,b,c分別是角A,B,C的對邊,向量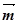 =(2sinB,2-cos2B),
=(2sinB,2-cos2B),
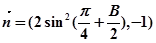 ,
,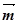 ⊥
⊥ .
.
(1)求角B的大小;
(2)若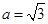 ,b=1,求c的值.
,b=1,求c的值.
(本小題滿分12分)
△ABC中,a,b,c分別是角A,B,C的對邊,且有sin2C+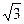 cos(A+B)=0.
cos(A+B)=0.
(1)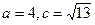 ,求△ABC的面積;
,求△ABC的面積;
(2)若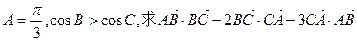 的值.
的值.
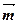 =(2sinB,2-cos2B),
=(2sinB,2-cos2B),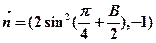 ,
,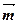 ⊥
⊥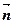 .
.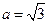 ,b=1,求c的值.
,b=1,求c的值.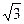 cos(A+B)=0.
cos(A+B)=0.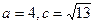 ,求△ABC的面積;
,求△ABC的面積;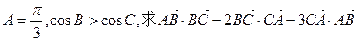 的值.
的值.(本小題滿分12分)
△A BC中,內角A、B、C的對邊分別為a、b、c
BC中,內角A、B、C的對邊分別為a、b、c
(I)若△ABC面積 =
=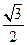 ,c=2,A=60°,求a,b的值
,c=2,A=60°,求a,b的值
(Ⅱ)若a=c·cosB,且b=c·sinA,試判斷△ABC的形狀
一、選擇題
1-6 C A B B B D 7-12 B C B B B C
二、填空
13. 4 14. .files/image195.gif) 15. 2 16.
15. 2 16..files/image197.gif)
三、解答題
17.(1)解:由.files/image199.gif)
有.files/image201.gif) ……6分
……6分
由.files/image203.gif) , ……8分
, ……8分
由余弦定理.files/image205.gif)
當.files/image207.gif) ……12分
……12分
.files/image208.jpg) ∴PB∥平面EFG. ………………………………3分
∴PB∥平面EFG. ………………………………3分
(2)解:取BC的中點M,連結GM、AM、EM,則GM//BD,
|