
題目列表(包括答案和解析)
已知函數f(x)=ax3+bx2+cx在x=±1處取得極值,且在x=0處的切線的斜率為-3.
(1)求f(x)的解析式;
(2)若過點A(2,m)可作曲線y=f(x)的三條切線,求實數m的取值范圍.
【解析】本試題主要考查了導數在研究函數中的運用。第一問,利用函數f(x)=ax3+bx2+cx在x=±1處取得極值,且在x=0處的切線的斜率為-3,得到c=-3 ∴a=1, f(x)=x3-3x
(2)中設切點為(x0,x03-3x0),因為過點A(2,m),所以∴m-(x03-3x0)=(3x02-3)(2-x0)分離參數∴m=-2x03+6x02-6
然后利用g(x)=-2x3+6x2-6函數求導數,判定單調性,從而得到要是有三解,則需要滿足-6<m<2
解:(1)f′(x)=3ax2+2bx+c
依題意
又f′(0)=-3
∴c=-3 ∴a=1 ∴f(x)=x3-3x
(2)設切點為(x0,x03-3x0),
∵f′(x)=3x2-3,∴f′(x0)=3x02-3
∴切線方程為y-(x03-3x0)=(3x02-3)(x-x0)
又切線過點A(2,m)
∴m-(x03-3x0)=(3x02-3)(2-x0)
∴m=-2x03+6x02-6
令g(x)=-2x3+6x2-6
則g′(x)=-6x2+12x=-6x(x-2)
由g′(x)=0得x=0或x=2
∴g(x)在(-∞,0)單調遞減,(0,2)單調遞增,(2,+∞)單調遞減.
∴g(x)極小值=g(0)=-6,g(x)極大值=g(2)=2
畫出草圖知,當-6<m<2時,m=-2x3+6x2-6有三解,
所以m的取值范圍是(-6,2).

已知函數 在
在 處取得極值2.
處取得極值2.
⑴ 求函數 的解析式;
的解析式;
⑵ 若函數 在區間
在區間 上是單調函數,求實數m的取值范圍;
上是單調函數,求實數m的取值范圍;
【解析】第一問中利用導數
又f(x)在x=1處取得極值2,所以 ,
,
所以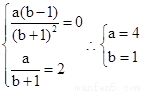
第二問中,
因為 ,又f(x)的定義域是R,所以由
,又f(x)的定義域是R,所以由 ,得-1<x<1,所以f(x)在[-1,1]上單調遞增,在
,得-1<x<1,所以f(x)在[-1,1]上單調遞增,在 上單調遞減,當f(x)在區間(m,2m+1)上單調遞增,則有
上單調遞減,當f(x)在區間(m,2m+1)上單調遞增,則有 ,得
,得
解:⑴ 求導 ,又f(x)在x=1處取得極值2,所以
,又f(x)在x=1處取得極值2,所以 ,即
,即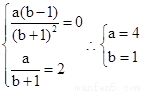 ,所以
,所以 …………6分
…………6分
⑵ 因為 ,又f(x)的定義域是R,所以由
,又f(x)的定義域是R,所以由 ,得-1<x<1,所以f(x)在[-1,1]上單調遞增,在
,得-1<x<1,所以f(x)在[-1,1]上單調遞增,在 上單調遞減,當f(x)在區間(m,2m+1)上單調遞增,則有
上單調遞減,當f(x)在區間(m,2m+1)上單調遞增,則有 ,得
,得 , …………9分
, …………9分
當f(x)在區間(m,2m+1)上單調遞減,則有
得 …………12分
…………12分
.綜上所述,當 時,f(x)在(m,2m+1)上單調遞增,當
時,f(x)在(m,2m+1)上單調遞增,當 時,f(x)在(m,2m+1)上單調遞減;則實數m的取值范圍是
時,f(x)在(m,2m+1)上單調遞減;則實數m的取值范圍是 或
或
 |
| y |
. |
| x |
. |
| y |
 |
| y |
. |
| x |
. |
| y |
| π |
| 6 |
| π |
| 6 |
| π |
| 12 |
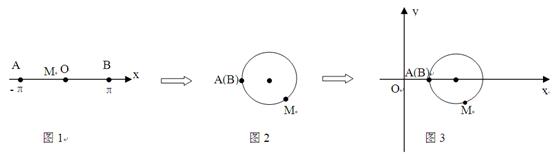
下圖展示了一個由區間(―π,π)到實數集R的映射過程:區間(―π,π)中的實數x對應軸上的點M(如圖1):將線段AB圍成一個圓,使兩端點A、B恰好重合(從A到B是逆時針,如圖2):再將這個圓放在平面直角坐標系中,使其圓心在x軸上,點A的坐標為(1,0)(如圖3),圖3中直線OM的斜率為k,則x的象就是k,記作k=¦(x).有下列判斷(1)¦(x)是奇函數;(2) ¦(x)是存在3個極值點的函數;(3) ¦(x)的值域是[―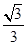 ,
,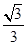 ];
];
(4) ¦(x)是區間(―π,π)上的增函數。其中正確的是
A、(1)(2) B、(1)(3) C、(2)(3) D、(1)(4)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com