
題目列表(包括答案和解析)
解關于 的不等式:
的不等式:

【解析】解:當 時,原不等式可變為
時,原不等式可變為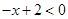 ,即
,即 (2分)
(2分)
當 時,原不等式可變為
時,原不等式可變為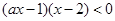
 (5分) 若
(5分) 若 時,
時, 的解為
的解為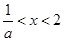 (7分)
(7分)
若 時,
時, 的解為
的解為 (9分) 若
(9分) 若 時,
時, 無解(10分) 若
無解(10分) 若 時,
時, 的解為
的解為 (12分綜上所述
(12分綜上所述
當 時,原不等式的解為
時,原不等式的解為
當 時,原不等式的解為
時,原不等式的解為
當 時,原不等式的解為
時,原不等式的解為
當 時,原不等式的解為
時,原不等式的解為
當 時,原不等式的解為:
時,原不等式的解為: 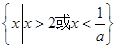
-1-
| ||||||
| 4 |
-1-
| ||||||
| 4 |
甲說:“只須不等式左邊的最小值不小于右邊的最大值”.
乙說:“把不等式變形為左邊含變量![]() 的函數,右邊僅含常數,求函數的最值”.
的函數,右邊僅含常數,求函數的最值”.
丙說:“把不等式兩邊看成關于![]() 的函數,作出函數圖像”.
的函數,作出函數圖像”.
參考上述解題思路,你認為他們所討論的問題的正確結論,即![]() 的取值范圍是 .
的取值范圍是 .
三個同學對問題“關于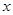 的不等式
的不等式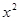 +25+|
+25+|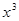 -5
-5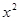 |≥
|≥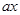 在[1,12]上恒成立,求實數
在[1,12]上恒成立,求實數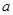 的取值范圍”提出各自的解題思路.
的取值范圍”提出各自的解題思路.
甲說:“只須不等式左邊的最小值不小于右邊的最大值”.
乙說:“把不等式變形為左邊含變量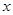 的函數,右邊僅含常數,求函數的最值”.
的函數,右邊僅含常數,求函數的最值”.
丙說:“把不等式兩邊看成關于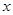 的函數,作出函數圖像”.
的函數,作出函數圖像”.
參考上述解題思路,你認為他們所討論的問題的正確結論,即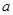 的取值范圍是
.
的取值范圍是
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com