題目列表(包括答案和解析)
如圖一，平面直角坐標系中有一張矩形紙片OABC，O為坐標原點，A點坐標為(10，0)，C點坐標為(0，6)，D是BC邊上的動點(與點B，C不重合)，現將△COD沿OD翻折，得到△FOD；再在AB邊上選取適當的點E，將△BDE沿DE翻折，得到△GDE，并使直線DG、DF重合。
(1)
如圖二，若翻折后點F落在OA邊上，求直線DE的函數關系式；(2)
設D(a，6)，E(10，b)，求b關于a的函數關系式，并求b的最小值；(3)
一般地，請你猜想直線DE與拋物線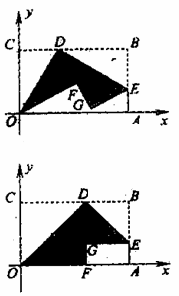
的公共點的個數，在圖二的情形中通過計算驗證你的猜想；如果直線DE與拋物線
始終有公共點，請在圖一中作出這樣的公共點。
一般地，如果函數y＝f(x)對于自變量取值范圍內的任意x，都有f(－x)＝－f(x)f那么y＝f(x)就叫做奇函數；如果函數y＝f(x)對于自變量取值范圍內的任意x，都有f(－x)＝f(x)，那么y＝f(x)就叫做偶函數．
例如：f(x)＝x3＋x．
當x取任意實數，
f(－x)＝(－x)3＋(－x)＝－x3－x＝－(x3＋x)
即f(－x)＝－f(x)
所以f(x)＝x3＋x為奇函數．
又如：f(x)＝|x|，
當x取任意實數時，f(－x)＝|－x|＝|x|＝f(x)，
即f(－x)＝f(x)
所以f(x)為偶函數．
問題：(1)下列函數：
①y＝x4；②y＝x2＋1；③y＝
；④y＝
；⑤y＝x＋
．
所有奇函數是________，所有偶函數是________(只填序號)；
(2)請你再分別寫出一個奇函數，一個偶函數．
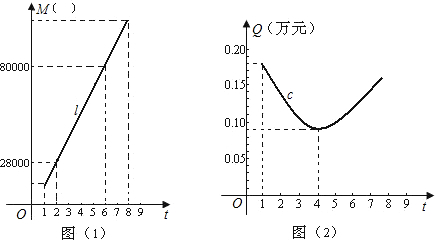
容積率t是指在房地產開發中建筑面積與用地面積之比，即t=
，為充分利用土地資源，更好地解決人們的住房需求，并適當的控制建筑物的高度，一般地容積率t不小于1且不大于8．一房地產開發商在開發某小區時，結合往年開發經驗知，建筑面積M(m2)與容積率t的關系可近似地用如圖(1)中的線段l來表示；1m2建筑面積上的資金投入Q(萬元)與容積率t的關系可近似地用如圖(2)中的一段拋物線段c來表示．
(1)
試求圖(1)中線段l的函數關系式，并求出開發該小區的用地面積；(2)
求出圖(2)中拋物線段c的函數關系式．容積率t是指在房地產開發中建筑面積與用地面積之比，即t=
，為充分利用土地資源，更好地解決人們的住房需求，并適當的控制建筑物的高度，一般地容積率t不小于1且不大于8.一房地產開發商在開發某小區時，結合往年開發經驗知，建筑面積M(m2)與容積率t的關系可近似地用如圖(1)中的線段l來表示；1 m2建筑面積上的資金投入Q(萬元)與容積率t的關系可近似地用如圖(2)中的一段拋物線段c來表示．
(1)
試求圖(1)中線段l的函數關系式，并求出開發該小區的用地面積；(2)
求出圖(2)中拋物線段c的函數關系式.
| M建筑面積 | S用地面積 |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com